Estimation Of Thermal Conductivity Of Fine Concrete With Recycled Pet Flakes By Two-Scale Homogenization Method

D. H. Nguyen; H. Le Quang; T.-D. Nguyen; A.-T.  Tran; T. A. Do

doi:10.6180/jase.202301_26(1).0011

Estimation Of Thermal Conductivity Of Fine Concrete With Recycled Pet Flakes By Two-Scale Homogenization Method

D.H. Nguyen This email address is being protected from spambots. You need JavaScript enabled to view it.¹, H. Le Quang², T.-D. Nguyen¹, A.-T. Tran³, and T. A. Do³

¹University of Transport and Communications, Department of Construction Materials, 3 Cau Giay, Dong Da, Hanoi, Vietnam
²MSME, Univ Gustave Eiffel, CNRS UMR 8208, Univ Paris Est Creteil, F-77454 Marne-la-Vallee, France
³University of Transport and Communications, Department of Bridge Engineering and Underground Infrastructure, 3 Cau Giay, Dong Da, Hanoi, Vietnam

Received: November 30, 2021
Accepted: February 16, 2022
Publication Date: April 7, 2022

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202301_26(1).0011

ABSTRACT

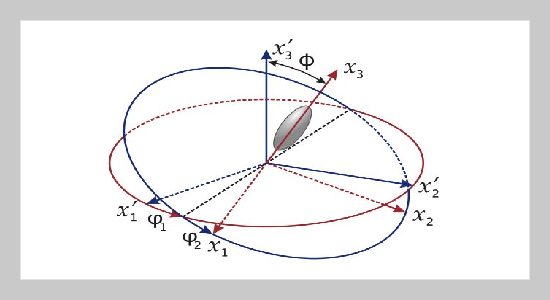
The present work aims to estimate the macroscopic thermal conductivity of fine concretes with recycled PET (Polyethylene terephthalate) flakes (Concrete withWaste Recycled Plastic - CWRP). To achieve this objective, the PET flakes are first assumed to exhibit a penny-shaped inclusion form whose aspect thickness/width (t/w) ratio is given as t/w = 1/33.33. These PET flakes are then supposed to be randomly distributed and oriented in a mortar phase consistuting of a cement paste (matrix) and silicious sand (inclusions). Next, a simple analytical two-scale homogenization method based both on different homogenization schemes and on the Eshelby’s solution is proposed to determine first at the mesoscopic scale the conductivity of the mortar and compute then at the macroscopic scale the effective conductivity of the fine concrete with recycled PET flakes. Finally, by varying the volume percentage of sand including 5, 10, 15, 30, 50 and 100 % of PET flakes, we show that the analytical results obtained for the effective thermal conductivity of CWRP by using the analytical homogenization method are in good agreement with experimental values.

Keywords: Homogenization method, Eshelby’s solution, Thermal conductivity, Fine concete with recycled pet flakes

REFERENCES

[1] E. Rahmani, M. Dehestani, M. Beygi, H. Allahyari, and I. Nikbin, (2013) “On the mechanical properties of concrete containing waste PET particles" Construction and Building Materials 47(Complete): 1302–1308. DOI: 10.1016/j.conbuildmat.2013.06.041.
[2] O. Yazoghli, R. Dheilly, and M. Quéneudec. “The valorisation of plastic waste: thermal conductivity of concrete formulated with PET”. In: 2005.
[3] Y.-W. Choi, D.-J. Moon, J.-S. Chung, and S.-K. Cho, (2005) “Effects of waste PET bottles aggregate on the properties of concrete" Cement and Concrete Research 35: 776–781. DOI: 10.1016/j.cemconres.2004.05.014.
[4] A. Poonyakan, M. Rachakornkij, M. Wecharatana, and W. Smittakorn, (2018) “Potential Use of Plastic Wastes for Low Thermal Conductivity Concrete" Materials 11: 1938. DOI: 10.3390/ma11101938.
[5] J. Eshelby, (1957) “The Determination of the Elastic Field Of An Ellipsoidal Inclusion and Related Problems" Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 241: DOI: 10.1098/rspa.1957.0133.
[6] A. Norris, (1985) “A Differential Scheme for the Effective Moduli of Composites" Mechanics of Materials 4: 1–16. DOI: 10.1016/0167-6636(85)90002-X.
[7] R. Christensen and K. Lo, (1979) “Solutions for Effective Shear Properties in Three Phase Sphere and Cylinder Models" Journal of the Mechanics and Physics of Solids 27: 315–330. DOI: 10.1016/0022-5096(79)90032-2.
[8] S. Li and G. Wang. Introduction to Micromechanics and Nanomechanics. 2018. DOI: 10.1142/8644.
[9] S. Torquato. Random Heterogeneous Materials: Microstructure and Macroscopic Properties. 55. 2002. DOI:10.1115/1.1483342.
[10] Zaoui. Materiaux heterogenes et composites. 2000.
[11] D.-H. Nguyen, H.-T. Le, H. Le Quang, and Q.-C. He, (2014) “Determination of the effective conductive properties of composites with curved oscillating interfaces by a two-scale homogenization procedure" Computational Materials Science 94: 150–162. DOI: 10.1016/j.commatsci.2014.03.014.
[12] D.-H. Nguyen, H. Le Quang, Q.-C. He, and T. An, (2021) “Generalized Hill-Mendel lemma and equivalent inclusion method for determining the effective thermal conductivity of composites with imperfect interfaces" Applied Mathematical Modelling 90: 624–649. DOI: 10.1016/j.apm.2020.09.026.
[13] H. Hatta and M. Taya, (1985) “Effective Thermal Conductivity of a Misoriented Short Fiber Composite" Journal of Applied Physics 58: 2478–2486. DOI: 10.1063/1.335924.
[14] H. Bunge, (1982) “Texture Analysis in Material Science": DOI: 10.1016/B978-0-408-10642-9.50019-2.
[15] T. Zhao, L. Zhang, and M. Huang, (2019) “Effective elasticity tensors of fiber-reinforced composite materials with 2D or 3D fiber distribution coefficients" Acta Mechanica 230: DOI: 10.1007/s00707-019-02485-w.