Makki A. Mohammed Salih1, Jaafer Hmood Eidi1, and Eman F. Mohommed This email address is being protected from spambots. You need JavaScript enabled to view it.1 1Department of Mathematics, College of Education, Almustansiriyah University-Baghdad-Iraq
Received:
June 1, 2021
Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.
Accepted:
November 14, 2021
Publication Date:
December 17, 2021
Download Citation:
||https://doi.org/10.6180/jase.202210_25(5).0001
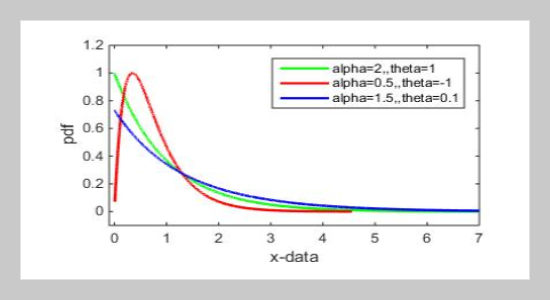
Several methods were used to estimate the two parameters of the transformed exponential distribution, which are the scale and the transmuted parameters, as well as its reliability function, namely, the moments method, modified moments, percentile, least squares, weighted least squares, and the maximum likelihood estimation, where the simulation method was used to generate the required data, where a sample size (n= 10, 30, 70 and 100), repeated sample (N= 1000), and the real value of the parameters for three experiments. The obtained results were compared by mean square error, and the results showed that, in general, the method of moments is the best in estimating the scale parameters, while the maximum likelihood estimation method is the best in estimating the transmuted parameter. Regarding reliability estimation, the method of moments is the most precise in the first experiment, while for the second and third experiments the percentile method is the best.ABSTRACT
Keywords:
Exponential Distribution, Estimation methods, Simulation, Mean square error
REFERENCES