Using the Radial Basis Function with the Novel Optimization Algorithms to Appraise the Pile Settlement rates

Yong  Zhang; Zhongyan  Luo; Qiuhong  Li; Daibing  Cheng; Wei  Tan

doi:10.6180/jase.202503_28(3).0007

Using the Radial Basis Function with the Novel Optimization Algorithms to Appraise the Pile Settlement rates

Yong ZhangThis email address is being protected from spambots. You need JavaScript enabled to view it., Zhongyan Luo, Qiuhong Li, Daibing Cheng, and Wei Tan

Department of Civil and Architectural Engineering, Nanchong Vocational and Technical College, Nanchong 637100, Sichuan, China

Received: April 26, 2023
Accepted: January 19, 2024
Publication Date: May 9, 2024

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202503_28(3).0007

Pile bridges, in particular, can be immunized by estimating Pile Settlement (PS) before operating construction projects. As one of the most critical factors in transportation projects, PS should be checked to avoid failure or reduce the failure risk. Available parameters of ground characteristics and pile physical data would assist us in having the project perspective over the operation period. Theoretical strategies to calculate the pile movement have attracted expert attention to model the PS, and artificial neural networks (ANN) are considered an efficient method used in many research types. The current study has utilized the Radial Basis Function (RBF) alongside Biogeography-Based Optimization (BBO) and a novel Flow Direction Algorithm (FDA) appraising the number of neurons integrated within hidden layer optimally to estimate the PS rates trained to models. The transportation project called KVMRT in Kuala Lumpur was examined. Regarding the mentioned models, two frameworks of RBF-BBO and RBF-FDA were developed to feed the in-situ inputs and, after training models, generate the PS value. As metrics evaluated the models, the RMSE indicator for RBF-BBO and RBF-FDA reached 0.500 and 0.650mm. Also, the MAE for RBF-BBO was calculated at 0.2583 with a 1% difference. The R2 correlation index showed the RBF-FDA as high-accurate with a 1.5% difference from BBO. Using a soft-based method instead of costly experiments can increase modeling accuracy with desirable results.

Keywords: Pile Settlement; Radial basis function; Biogeography-Based Optimization; novel Flow Direction Algorithm; RMSE.

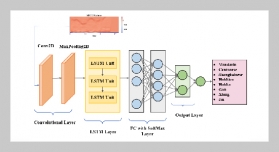
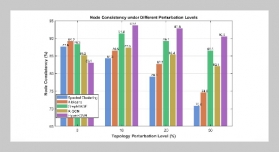
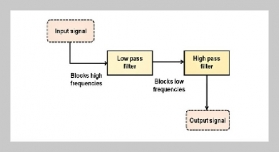
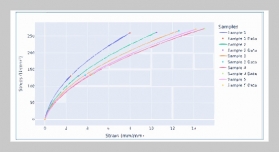
[1] E. Momeni, R. Nazir, D. J. Armaghani, and H. Maizir, (2015) “Application of artificial neural network for predicting shaft and tip resistances of concrete piles" Earth Sciences Research Journal 19: 85–93. DOI: 10.15446/esrj.v19n1.38712.
[2] E. Momeni, H. Maizir, N. Gofar, and R. Nazir, (2013) “Comparative study on prediction of axial bearing capacity of driven piles in granular materials" Jurnal Teknologi 61: 15–20. DOI: 10.11113/jt.v61.1777.
[3] F. Milad, T. Kamal, H. Nader, and O. E. Erman, (2015) “New method for predicting the ultimate bearing capacity of driven piles by using Flap number" KSCE Journal of Civil Engineering 19: 611–620. DOI: 10.1007/s12205-013-0315-z.
[4] R. Nazir, E. Momeni, N. G. Nurly, and H. Maizir, (2013) “Numerical modeling of skin resistance distribution with depth in piles" Electron J Geotech Eng 18: 2477–2488.
[5] E. Momeni, M. B. Dowlatshahi, F. Omidinasab, H. Maizir, and D. J. Armaghani, (2020) “Gaussian process regression technique to estimate the pile bearing capacity" Arabian Journal for Science and Engineering 45: 8255–8267. DOI: 10.1007/s13369-020-04683-4.
[6] I.-M. Lee and J.-H. Lee, (1996) “Prediction of pile bearing capacity using artificial neural networks" Computers and geotechnics 18: 189–200. DOI: 10.1016/0266- 352X(95)00027-8.
[7] W. F. Che, T. M. H. Lok, S. C. Tam, and H. NovaisFerreira, (2003) “Axial capacity prediction for driven piles at Macao using artificial neural network":
[8] H. Liu, T. J. Li, and Y. F. Zhang, (1997) “The application of artificial neural networks in estimating the pile bearing capacity":
[9] J.-K. Hu, (2022) “Estimation of pile settlement applying hybrid ALO-MLP and GOA-MLP approaches" Journal of Applied Science and Engineering 25: 1239–1255. DOI: 10.6180/jase.202212_25(6).0019.
[10] Y. Zhang, (2022) “Pile settlement prediction applying hybrid ALO-SVR and BBO-SVR approaches" Multiscale and Multidisciplinary Modeling, Experiments and Design 5: 243–253.
[11] M. Shanbeh, D. Najafzadeh, and S. A. H. Ravandi, (2012) “Predicting pull-out force of loop pile of woven terry fabrics using artificial neural network algorithm" Industria Textila 63: 37–41.
[12] A. M. Hanna, G. Morcous, and M. Helmy, (2004) “Efficiency of pile groups installed in cohesionless soil using artificial neural networks" Canadian Geotechnical Journal 41: 1241–1249.
[13] A. T. C. Goh, (1996) “Pile driving records reanalyzed using neural networks" Journal of Geotechnical Engineering 122: 492–495.
[14] C. I. Teh, K. S. Wong, A. T. C. Goh, and S. Jaritngam, (1997) “Prediction of pile capacity using neural networks" Journal of computing in civil engineering 11: 129–138.
[15] A. A. Jebur, W. Atherton, R. M. A. Khaddar, and E. Loffill, (2021) “Artificial neural network (ANN) approach for modelling of pile settlement of open-ended steel piles subjected to compression load" European Journal of Environmental and Civil Engineering 25: 429– 451. DOI: 10.1080/19648189.2018.1531269.
[16] D. J. Armaghani, P. G. Asteris, S. A. Fatemi, M. Hasanipanah, R. Tarinejad, A. S. A. Rashid, and V. V. Huynh, (2020) “On the use of neuro-swarm system to forecast the pile settlement" Applied Sciences 10: 1904.
[17] H. Moayedi, A. Osouli, D. T. Bui, L. K. Foong, H. Nguyen, and B. Kalantar, (2019) “Two novel neuralevolutionary predictivetechniques of dragonfly algorithm (DA) andbiogeography-based optimization (BBO) forlandslide susceptibility analysis":
[18] A. Ismail and D.-S. Jeng, (2011) “Modelling load–settlement behaviour of piles using high-order neural network (HON-PILE model)" Engineering Applications of Artificial Intelligence 24: 813–821.
[19] A. K. Bansal, R. Kumar, and R. A. Gupta, (2013) “Economic analysis and power management of a small autonomous hybrid power system (SAHPS) using biogeography based optimization (BBO) algorithm" IEEE Transactions on Smart Grid 4: 638–648.
[20] Q. Niu, L. Zhang, and K. Li, (2014) “A biogeographybased optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells" Energy conversion and management 86: 1173–1185.
[21] M. Ahmadlou, M. Karimi, S. Alizadeh, A. Shirzadi, D. Parvinnejhad, H. Shahabi, and M. Panahi, (2019) “Flood susceptibility assessment using integration of adaptive network-based fuzzy inference system (ANFIS) and biogeography-based optimization (BBO) and BAT algorithms (BA)" Geocarto International 34: 1252–1272.
[22] L. Abualigah, K. H. Almotairi, M. A. Elaziz, M. Shehab, and M. Altalhi, (2022) “Enhanced Flow Direction Arithmetic Optimization Algorithm for mathematical optimization problems with applications of data clustering" Engineering Analysis with Boundary Elements 138: 13–29.
[23] N. Fehn, W. A. Wall, and M. Kronbichler, (2019) “Modern discontinuous Galerkin methods for the simulation of transitional and turbulent flows in biomedical engineering: a comprehensive LES study of the FDA benchmark nozzle model" International Journal for Numerical Methods in Biomedical Engineering 35: e3228.
[24] K. Jain, (2020) “Efficacy of the FDA nozzle benchmark and the lattice Boltzmann method for the analysis of biomedical flows in transitional regime" Medical & Biological Engineering & Computing 58: 1817–1830. DOI: 10.1007/s11517-020-02188-8.
[25] H. Bendu, B. Deepak, and S. Murugan, (2016) “Application of GRNN for the prediction of performance and exhaust emissions in HCCI engine using ethanol" Energy conversion and management 122: 165–173.
[26] V. K. Alilou and F. Yaghmaee, (2015) “Application of GRNN neural network in non-texture image inpainting and restoration" Pattern Recognition Letters 62: 24– 31. DOI: 10.1016/j.patrec.2015.04.020.
[27] A. Zendehboudi and A. Tatar, (2017) “Utilization of the RBF network to model the nucleate pool boiling heat transfer properties of refrigerant-oil mixtures with nanoparticles" Journal of Molecular Liquids 247: 304–312.
[28] M. A. Shahin, H. R. Maier, and M. B. Jaksa, (2002) “Predicting settlement of shallow foundations using neural networks" Journal of geotechnical and geoenvironmental engineering 128: 785–793. DOI: 10.1061/(ASCE)1090-0241(2002)128:9(785).
[29] A. W. Hatheway, (2009) “The complete ISRM suggested methods for rock characterization, testing and monitoring; 1974–2006":
[30] H. Karami, M. V. Anaraki, S. Farzin, and S. Mirjalili, (2021) “Flow direction algorithm (FDA): a novel optimization approach for solving optimization problems" Computers & Industrial Engineering 156: 107224. DOI: 10.1016/j.cie.2021.107224.
[31] D. Simon, (2008) “Biogeography-based optimization" IEEE transactions on evolutionary computation 12: 702–713.
[32] R. Rarick, D. Simon, F. E. Villaseca, and B. Vyakaranam. “Biogeography-based optimization and the solution of the power flow problem”. In: IEEE, 2009, 1003–1008. DOI: 10.1109/ICSMC.2009.5346046.
[33] D. E. Goldberg, (2000) “The design of innovation: Lessons from genetic algorithms, lessons for the real world" Technological Forecasting and Social Change 64: 7–12. DOI: 10.1016/s0040-1625(99)00079-7.
[34] W. Sun, D. Liu, J. Wen, and Z. Wu, (2017) “Modeling of MEMS gyroscope random errors based on grey model and RBF neural network" J. Navig. Position 5: 9–13.
[35] S. Seshagiri and H. K. Khalil, (2000) “Output feedback control of nonlinear systems using RBF neural networks" IEEE Transactions on Neural Networks 11: 69–79.
[36] G. Pazouki, E. M. Golafshani, and A. Behnood, (2022) “Predicting the compressive strength of self-compacting concrete containing Class F fly ash using metaheuristic radial basis function neural network" Structural Concrete 23: 1191–1213.