Xiaomei Yang¹, Jianchao Zen This email address is being protected from spambots. You need JavaScript enabled to view it.^1,2 and Yu Zhang¹

¹Division of Industrial and System Engineering, Taiyuan University of Science & Technology, Taiyuan 030024, P.R. China
²School of Computer Science and Control Engineering, North University of China, Taiyuan 030051, P.R. China

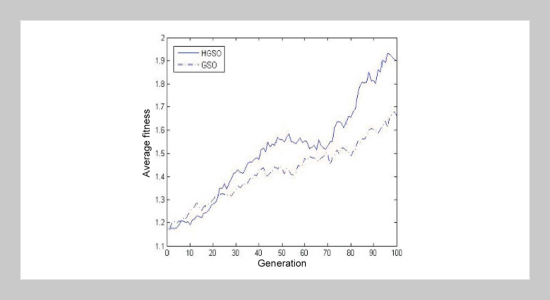
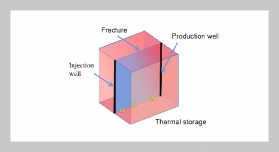
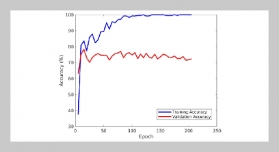
REFERENCES

1. [1] Krishnand, K. N. and Ghose, D., “Detection of Multiple Source locations Using a Glowworm Metaphor with Applications to Collective Robotics,” Proceedings of IEEE Swarm Intelligence Symposium, Pasadena, CA, Jun 810, (2005). doi: 10.1109/SIS.2005. 1501606
2. [2] Jayakumar, D. N. and Venkatesh, P., “Glowworm Swarm Optimization Algorithm with Topsis for Solving Multiple Objective Environmental economic Dispatch Problem,” Applied Soft Computing, Vol. 23, pp. 375386 (2014). doi: 10.1016/j.asoc.2014.06.049
3. [3] Cui, H., Feng, J., Guo, J. and Wang, T., “A Novel Single Multiplicative Neuron Model Trained by an Improved Glowworm Swarm Optimization Algorithm for Time Series Prediction,” Knowledge-Based Systems, Vol. 88, pp. 195209 (2015). doi: 10.1016/j. knosys.2015.07.032
4. [4] Zhou, Y., Zhou, G. and Zhang, J., “A Hybrid Glowworm Swarm Optimization Algorithm to Solve Constrained Multimodal Functions Optimization,” Optimization, Vol. 64, No. 4, pp. 10571080 (2015). doi: 10.1080/02331934.2013.793329
5. [5] Wu, B., Qian, C., Ni, W. and Fan, S., “The Improvement of Glowworm Swarm Optimization for Continuous Optimization Problems,” Expert Systems with Applications, Vol. 39, No. 7, pp. 63356342 (2012). doi: 10.1016/j.eswa.2011.12.017
6. [6] Zhou, Y. Q. and Huang, Z. X., “Artificial Glowworm Swarm Optimization Algorithm for TSP,” Control and Decision, Vol. 27, No. 12, pp. 18161821 (2012).
7. [7] Si, X., Zheng, Y. and An, X., “Minimizing the Number of Late Orders with Multiple Job Classes,” Acta Automatica Sinica, Vol. 26, No. 6, pp. 845847 (2000). (Chinese)
8. [8] Zhong, X., Ou, J. and Wang, G., “Order Acceptance and Scheduling with Machine Availability Constraints,” European Journal of Operational Research, Vol. 232, No. 3, pp. 435441 (2014). doi: 10.1016/j.ejor.2013. 07.032
9. [9] Wei, J. and Ma, Y. S., “Design of a Feature-based Order Acceptance and Scheduling Module in an ERP System,” Computers in Industry, Vol. 65, No. 1, pp. 6478 (2014). doi: 10.1016/j.compind.2013.07.009
10. [10] Baker, K. R. and Trietsch, D., Principles of Sequencing and Scheduling, John Wiley & Sons Inc, New York (2013).
11. [11] Li, X., Shao, Z. and Qian, J., “An Optimizing Method Based on Autonomous Animats: Fish-swarm Algorithm,” System Engineering Theory and Practice, Vol. 22, No. 11, pp. 3238 (2002).
12. [12] Cheng, T. C. E., Wu, C. C., Chen, J. C. and Wu, W. H., “Two-machine Flowshop Scheduling with a Truncated Learning Function to Minimize the Makespan,” International Journal of Production Economics, Vol. 141, No. 1, pp. 7986 (2013). doi: 10.1016/j.ijpe.2012.03. 027