Shape Optimization of Single-Chamber Mufflers with Side Inlet/Outlet by Using Boundary Element Method, Mathematic Gradient Method and Genetic Algorithm

Min-Chie Chiu; Long-Jyi  Yeh; Ying-Chun  Chang; Tian-Syung  Lan

doi:10.6180/jase.2009.12.1.09

Shape Optimization of Single-Chamber Mufflers with Side Inlet/Outlet by Using Boundary Element Method, Mathematic Gradient Method and Genetic Algorithm

Min-Chie Chiu This email address is being protected from spambots. You need JavaScript enabled to view it.¹, Long-Jyi Yeh² , Ying-Chun Chang² and Tian-Syung Lan³

¹Department of Automatic Control Engineering, Chungchou Institute of Technology, Changhua, Taiwan 510, R.O.C.
²Department of Mechanical Engineering, Tatung University, Taipei, Taiwan, R.O.C.
³Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan, R.O.C.

Received: August 28, 2006
Accepted: July 14, 2008
Publication Date: March 1, 2009

Download Citation: ||https://doi.org/10.6180/jase.2009.12.1.09

ABSTRACT

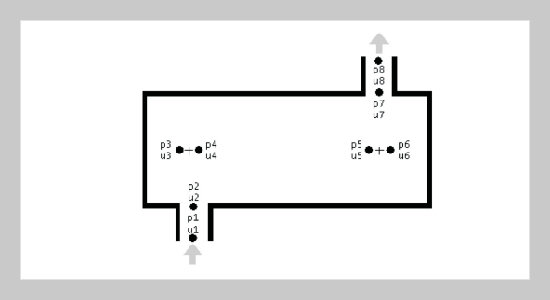
This paper is trying to build up the theoretical four-pole matrices for the single-chamber mufflers equipped with side inlet/outlet duct. In addition, by using the BEM simulation and the experimental works on silencers, the accuracy of above theoretical solution can be verified and reassured, accordingly. Moreover, applying the numerical optimizations of genetic algorithm (GA) and three kinds of mathematic gradient method – interior penalty function method (IPFM), exterior penalty function method (EPFM) and feasible direction method (FDM), the optimal design of silencers under constrained space can then be achieved. In this paper, considering the flowing effect, the theoretical scalar function of muffler’s noise reduction is firstly deduced by using four-pole matrices method on the basis of onedimensional plane wave theorem. Moreover, a numerical case of muffler’s shape optimization in dealing with the elimination of pure tone noise of 500 Hz under space constraints is introduced. Before optimizations being performed, the effective design variables can be selected by the computer-aided sensitivity analysis of design parameters in Matlab package. Besides, the starting points have been initialized first and then later taken into the Gradient methods for further optimization. By using Gradient Methods and GA Method, several better design data are obtained. Consequently, the best design parameter with highest STL may be determined within them.

Keywords: Single-Chamber Muffler with Side Inlet/Outlet, Four-Pole Transfer Matrix, Mathematic Gradient Method, Boundary Element Method, Genetic Algorithm, Sound Transmission Loss, Optimal Design

REFERENCES

[1] Davis, D. D., Stokes, J. M. and Moorse, Steven, L., “Theoretical and Experimental Investigation of Mufflers with Components on Engine Muffler Design,” NACA Report, p. 1192 (1954).
[2] Prasad, M. G. and Crocker, M. J., “Studies of Acoustical Performance of a Multi-cylinder Engine Exhaust Muffler System,” Journal of Sound and Vibration, Vol. 90, pp. 491508 (1983).
[3] Prasad, M. G., “A Note on Acoustic Plane Waves in a Uniform Pipe with Mean Flow,” Journal of Sound and Vibration, Vol. 95, pp. 284290 (1984).
[4] Munjal, M. L. and Prasad, M. G., “Transfer Matrix of a Uniform Tube with Moving Medium and Linear Temperature Gradient,” J. Acoust. Soc. Am., Vol. 80, pp. 15011506 (1986).
[5] Munjal, M. L., Acoustics of Ducts and Mufflers with Application to Exhaust and Ventilation System Design, John Wiley & Sons, New York (1987).
[6] Munjal, M. L., “Plane Wave Analysis of Side Inlet/ Outlet Chamber Mufflers with Mean Flow,” Applied Acoustics, Vol. 52, pp. 165175 (1997).
[7] Bernhard, Robert J., “Shape Optimization of Reactive Mufflers,” Noise Control Engineering Journal, Vol. 27, pp. 1017 (1986).
[8] Yeh, L. J., Chiu, M. C. and Lay, G. J., “Computer Aided Design on Single Expansion Muffler under Space Constraints,” The 19th National Conference on C.S.M.E, C7, pp. 625633 (2002).
[9] Vanderplaats, Garret N., Numerical Optimization Techniques for Engineering Design: With Applications, McGraw-Hill, New York, pp. 71195 (1984).
[10] Chang, Y. C., Yeh, L. J., Chiu, M. C. and Lai, G. J., “Shape Optimization on Constrained Single-Layer Sound Absorber by Using GA Method and Mathematical Gradient Methods,” Journal of Sound and Vibration, Vol. 1286/4-5, pp. 941961 (2005).
[11] Holland, J., Adaptation in Natural and Artificial System, Ann Arbor, University of Michigan Press (1975).
[12] Jong, D., An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Doctoral thesis, Dept. Computer and Communication Sciences, Ann Arbor, University of Michigan (1975).
[13] Goldberg, D. E., Genetic Algorithm in Search, Optimization and Machine Learning, Massachusets, Addison-Wesley (1988).