Rainfield Y. Yen This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Department of Electrical Engineering, Tamkang University, Tamsui, Taiwan 251, R.O.C.

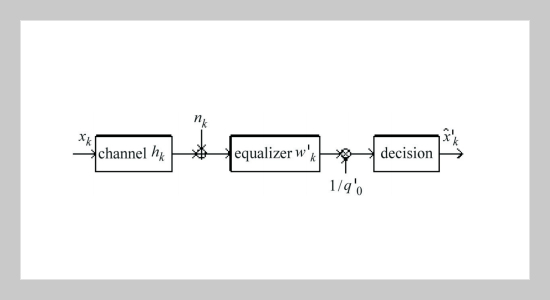
REFERENCES

1. [1] Proakis, J. G., Digital Communications, 4th ed. McGraw-Hill, New York (2001).
2. [2] Gitlin, R. D., Hayes, J. F. and Weinstein, S. B., Data Communication Principles, Plenum (1992).
3. [3] Haykin, S., Adaptive Filter Theory, 4th ed. PrenticeHall, Upper Saddle River, NJ (2002).
4. [4] Saltzburg, B. R., “Intersymbol Interference Error Bounds with Application to Ideal Bandlimited Signaling,” IEEE Trans. Inform. Theory, Vol. IT-14, pp. 563
   568 (1968).
5. [5] Lee, E. A. and Messerschmitt, D. G., Digital Communications, 2nd ed. Kluwer, Boston, MA (1994).
6. [6] Cioffi, J. M., Dudevoir, G. P., Eyuboglu, M. V. and Forney, Jr., G. D., “MMSE Decision-Feedback Equalizera and Coding-Part I: Equalization Results,” IEEE Trans. Commun., Vol. 43, pp. 2582
   2594 (1995).
7. [7] Lugannani, R., “Intersymbol Interference and Probability of Error in Digital Systems,” IEEE Trans. Inform. Theory, Vol. IT-15, pp. 682
   688 (1969).
8. [8] Ho, E. Y. and Yeh, Y. S., “A New for Evaluating the Error Probability in the Presence of Intersymbol Interference and Additive Gaussian Noise,” Bell Syst. Tech. J., Vol. 49, pp. 2249
   2265 (1970).
9. [9] Shimbo, O. and Celebiler, M., “The Probability of Error Due to Intersymbol Interference and Gaussian Noise in Digital Communication Systems,” IEEE Trans. Commun. Technol., Vol. COM-19, pp. 113
   119 (1971).
10. [10] Glave, F. E., “An Upper Bound on the Probability of Error Due to Intersymbol Interference for Correlated Digital Signals,” IEEE Trans. Inform. Theory, Vol. IT-18, pp. 356
    363 (1972).
11. [11] Yao, K., “On Minimum Average Probability of Error Expression for Binary Pulse-Communication System with Intersymbol Interference,” IEEE Trans. Inform. Theory, Vol. IT-18, pp. 528
    531 (1972).
12. [12] Yao, K. and Tobin, R. M., “Moment Space Upper and Lower Error Bounds Digital Systems with Intersymbol Interference,” IEEE Trans. Inform. Theory, Vol. IT-22, pp. 65
    74 (1976).
13. [13] Salz, J., “Optimum Mean-Square Decision-Feedback Equalization,” Bell Syst. Tech. J., Vol. 52, pp. 1341
    1373 (1973).
14. [14] Chen, S., Mulgrew, B., Chng, E. S. and Gibson, G. J., “Space Translation Properties and the Minimum-BER Linear-Combiner DFE,” IEE Proc.-Commun., Vol. 145, pp. 316
    322 (1998).
15. [15] Chen, S. and Mulgrew, B., “Minimum-SER LinearCombiner Decision Feedback Equalizer,” IEE Proc. - Commun., Vol. 146, pp. 347
    353 (1999).
16. [16] Chen, S., Samingan, A. K., Mulgrew, B. and Hanzo, L., “Adaptive Minimum-BER Linear Multiuser Detection for DS-CDMA Signals in Multipath Channels,” IEEE Trans. Signal Process., Vol. 49, pp. 1240
    1247 (2001).
17. [17] Chen, S., Hanzo, L. and Mulgrew, B., “Adaptive Minimum Symbol-Error-Rate Decision Feedback Equalization for Multilevel Pulse-Amplitude Modulation,” IEEE Trans. Signal Process., Vol. 52, pp. 2092
    2101 (2004).
18. [18] Yeh, C.-C. and Barry, J. R., “Adaptive Minimum BitError Rate Equalization for Binary Signaling,” IEEE Trans. Commun., Vol. 48, pp. 1226
    1235 (2000).
19. [19] , “Adaptive Minimum Symbol-Error Rate Equalization for Quadrature-Amplitude Modulation,” IEEE Trans. Signal Process., Vol. 51, pp. 3263
    3269 (2003).
20. [20] Liu, H. Y. and Yen, R. Y., “Channel Equalization Using Biased and Unbiased Minimum Error Rate Criteria,” IEICE Trans. Fundamentals, Vol. E87-A, pp. 605
    609 (2004).
21. [21] Yen, R. Y., Liu, H. Y., Li, C. W. and Cheng, W. C., “The Adaptive MSINR Algorithm to Improve Error Rate for Channel Equalization,” Signal Processing, Vol. 86, pp. 1984
    1991 (2006).
22. [22] Yen, R. Y., “Stochstic Unbiased Minimum Mean Error Rate Algorithm for Decision Feedback Equalizers,” IEEE Trans. Signal Processing, Vol. 55, pp. 4758
    4766 (2007).