Robustly Decentralized Hꚙ Controller with Variance Constraint Design for Large-Scale Stochastic Uncertain Time-Delay Systems via LMI Approach

Wen-Ben Wu; Pang-Chia Chen; Gong  Chen; Koan-Yuh Chang; Yeong-Hwa Chang

doi:10.6180/jase.2009.12.1.06

Robustly Decentralized Hꚙ Controller with Variance Constraint Design for Large-Scale Stochastic Uncertain Time-Delay Systems via LMI Approach

Wen-Ben Wu This email address is being protected from spambots. You need JavaScript enabled to view it.¹, Pang-Chia Chen² , Gong Chen³ , Koan-Yuh Chang⁴ and Yeong-Hwa Chang⁵

¹Department of Electrical Engineering, Chin-Min Institute of Technology, Miaoli, Taiwan 351, R.O.C.
²Department of Electrical Engineering, Kao Yuan University, Kaohsiung, Taiwan 821, R.O.C.
³Department of Electrical and Electronic Engineering, National Defense University, Taoyuan, Taiwan 335, R.O.C.
⁴Department of Electronic Engineering, Chienkuo Technology University, Changhua City, Taiwan 500, R.O.C.
⁵Department of Electrical Engineering, Chang Gung University, Taoyuan, Taiwan 333, R.O.C.

Received: September 6, 2007
Accepted: June 3, 2008
Publication Date: March 1, 2009

Download Citation: ||https://doi.org/10.6180/jase.2009.12.1.06

ABSTRACT

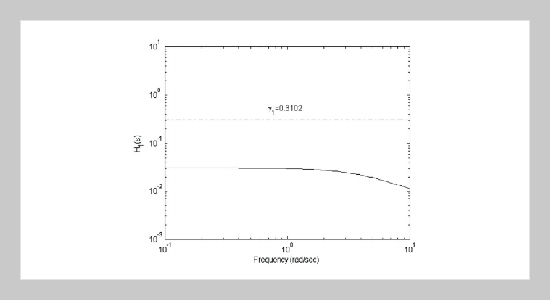
The present paper investigates the problem of robustly decentralized H_∝ state feedback controller with state variance constraint design for a class of stochastic large-scale uncertain time-delay systems. The considered time-delay parameters appear in the interconnections between individual subsystems and uncertainties are allowed to be unstructured but time-varying and normbounded. The sufficient conditions of the desired state feedback controller, which satisfies the performance level constraint in terms of H_∝ norm for noise attenuation and upper bound of individual state variance constraint for considering its state energy limitation, are based on the LyapunovKrasovskii stability theory and utilizing the decentralized scheme to be derived in terms of linear matrix inequalities (LMIs). The effectiveness of the proposed approach is illustrated by a numerical example.

Keywords: LMI, Large-Scale Uncertain Time-Delay System, Robustly Decentralized Control, Variance Constraint

REFERENCES

[1] Mao, X., Kololeva, N. and Rodkina, A., “Robust Stability of Uncertain Stochastic Differential Delay Equation,” Systems and Control Letters, Vol. 35, pp. 325 336 (1998).
[2] Verriest, E. I. and Florchinger, P., “Stability of Stochastic Systems with Uncertain Time Delays,” System and Control Letters, Vol. 24, pp. 4147 (1995).
[3] Florchinger, P., “Lyapunov-Like Techniques for Stochastic Stability,” Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, Florida, pp. 11451150 (1994).
[4] Sandell, N. R., Varaiya, P., Athans, M. and Safonov, M. G., “Survey of Decentralized Control Method for Large-Scale System,” IEEE Trans. Automatic Control, Vol. 23, pp. 108128 (1978).
[5] Jamshidi, M., Large-scale system: modeling, control, and fuzzy logic. Prentice-Hall, New Jersey, pp. 229 280 (1997).
[6] Wu, W. B., Chen, P. C., Chen, G., Chang, K. C. and Chang, Y. H., “Multiobjective State-Feedback Control for Stochastic Large-Scale System via LMI Approach,” JOURNAL CHUNG CHENG INSTITUTE OF TECHNOLOGY, Vol. 34, pp. 120 (2006).
[7] Xie, S. and Xie, L., “Stabilization of Class of Uncertain Large-Scale Stochastic System with Time Delays,” Automatica, Vol. 36, pp. 161167 (2000).
[8] Xu, S. and Chen, T., “Robust H Control for Uncertain Stochastic System with State Delay,” IEEE Trans. on Automatic Control, Vol. 47, pp. 20892094 (2002).
[9] Xie, S., Xie, L. and Wen, C., “Decentralized H Output Feedback Control of Interconnected Time-Delay Systems,” Proceedings of the American Control Conference, Chicago, Illinois, pp. 824828 (2000).
[10] Collins, E. G. and Skelton, R. E., “A Theory of State Covariance Assignment for Discrete System,” IEEE Trans. Automatic Control, Vol. 32, pp. 3541 (1987).
[11] Sreeram, V. and Liu, W. Q., “Theory of State Covariance Assignment for Linear Single-Input System,” IEE Proc.-Control Theory and Applications, Vol. 41, pp. 289295 (1996).
[12] Wu, W. B., Chen, P. C., Chen, G. and Chang, Y. H., “LMI Decentralized Controller Design for Stochastic Large-Scale Time-Delay Systems,” Proceeding of the 2004 IEEE International Conference on Control Applications, Taipei, R. O. C., pp. 632637 (2004).
[13] Scherer, C., Gahinet, P. and Chilali, M., “Multiobjective Output-Feedback Control via LMI Optimization,” IEEE Trans. Automatic Control, Vol. 42, pp. 896911 (1997).
[14] Vandenberghe, L. V. and Balakrishnan, V. K., “Algorithm and Software for LMI Problems in Control,” IEEE Control Systems Lecture Notes, Vol. 17, pp. 8995 (1997).
[15] Chilali, M., and Gahient, P., “H Design with Pole Placement Constraints: An LMI Approach,” IEEE Trans. Automatic Control, Vol. 41, pp. 358367 (1996).
[16] Chilali, M. and Gahient, P., “Robust Pole Placement in LMI Regions,” IEEE Trans. on Automatic Control, Vol. 44, pp. 22572269 (1999).
[17] Hu, Z., “Decentralized Stabilization of Large-Scale Interconnected Systems with Delays,” IEEE Trans. on Automatic Control, Vol. 39, pp. 180182 (1994).
[18] Boyd, S., Ghaoui, L. E., Feron, E. and Balakrishnan, V., Linear matrix inequality in system and control theory, SIAM, Philadelphia, pp. 735 (1994).
[19] Gahinet, P., Nemirovski, A., Laub, A. J. and Chilali, M., LMI control toolbox for use with MATLAB, The Math Work Inc., Natick, Massachusetts, p. 4-1 to p. 5-6 (1995).
[20] Kharitonov, V. L., and Zhabko, A. P., “LyapunovKrasovskii Approach to the Robust Stability Analysis of Time-Delay Systems,” Automatica, Vol. 39, pp. 1520 (2003).
[21] Wang, Y., Xie, L. and De Souza, C. E., “Robust Control of a Class of Uncertain Nonlinear System,” System and Control Letters, Vol. 19, pp. 139149 (1992).