I. K. Bousserhane This email address is being protected from spambots. You need JavaScript enabled to view it.1, A. Hazzab1 , M. Rahli2 , B. Mazari1 and M. Kamli2 1University center of Bechar, B.P 417 Bechar 08000, Algeria
2University of Sciences and Technology of Oran, Algeria
Received:
March 21, 2006
Accepted:
January 11, 2007
Publication Date:
March 1, 2009
Download Citation:
||https://doi.org/10.6180/jase.2009.12.1.03
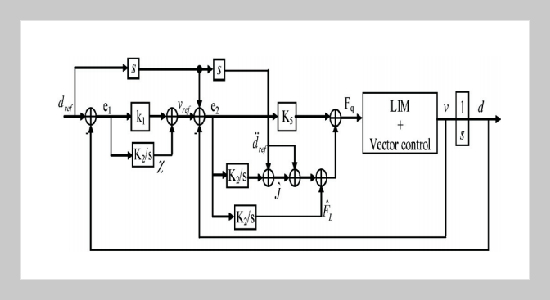
In this paper, an adaptive backstepping control system with a fuzzy integral action is proposed to control the mover position of a linear induction motor (LIM) drive. First, the indirect field oriented control LIM is derived. Then, an integral backstepping design for indirect field oriented control of LIM is proposed to compensate the uncertainties which occur in the control. Finally, the adaptive backstepping controller with fuzzy integral action is investigated where a simple fuzzy inference mechanism is used to achieve the mover position tracking objective under the mechanical parameters uncertainties. The performance of the proposed control scheme was demonstrated through simulations. The numerical validation results of the proposed scheme have presented good performances compared to the adaptive backstepping control with integral action.ABSTRACT
Keywords:
Linear Induction Motor, Field-Oriented Control, Adaptive Backstepping, Fuzzy Integral-Backstepping
REFERENCES