Study of Numerical Simulation Applying to the Design of an Orifice with High-Velocity Waterjet

Fu-Cheng Yang; Sheau-Wen Shiah; Tzeng-Yuan Heh; Chan-Yung Jen; Wen-I  Chang

doi:10.6180/jase.2008.11.2.06

Study of Numerical Simulation Applying to the Design of an Orifice with High-Velocity Waterjet

Fu-Cheng Yang This email address is being protected from spambots. You need JavaScript enabled to view it.¹, Sheau-Wen Shiah² , Tzeng-Yuan Heh² , Chan-Yung Jen³ and Wen-I Chang⁴

¹Graduate School of Defense Science, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan 335, R.O.C.
²Department of Power Vehicle and System Engineering, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan 335, R.O.C.
³Department of Mechanical and Marine Engineering, Naval Academy, Kaohsiung, Taiwan 813, R.O.C.
⁴Duo De Company of Limited Liability, Taoyuan, Taiwan 325, R.O.C.

Received: April 11, 2007
Accepted: August 29, 2007
Publication Date: June 1, 2008

Download Citation: ||https://doi.org/10.6180/jase.2008.11.2.06

ABSTRACT

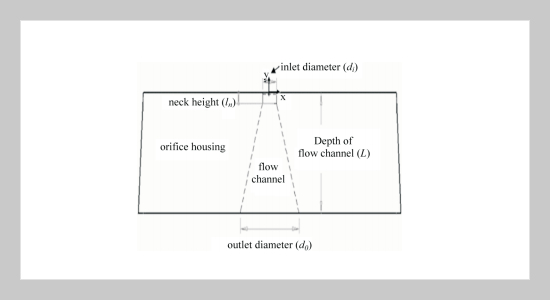
The purpose of this paper is using numerical simulation method to discuss the influences of high-velocity waterjet on different types of orifice which is made of diamond. Not only we aim at establishing the model of analysis to the orifice geometry but also change the design conditions of the orifices in order to find the optimal orifice shape. During the numerical simulation, a two-dimensional axial-symmetric model is established first, and then some practical geometric parameters are considered for the orifice, including flow channel with 0.5 mm in depth, 0.1 mm to 0.56 mm for the diameters of inlet and outlet, and 0.005 mm to 0.346 mm for the neck height. The analytic results can show the pressure and velocity distributions of high-velocity waterjets in the orifices under different conditions and can be used for assessment of orifice geometric design. Through this study, it is expected to know more physical insight about the effect of high-velocity waterjet on orifice geometry and further to improve the life cycle of orifice.

Keywords: Design of Orifices, High-Velocity Waterjets, Numerical Simulation

REFERENCES

[1] Kahlman, L., Karlsson, S., Gralsson, R. and Nilson, C. G., “Wear and Machining of Engineering Ceramics by Abrasive Waterjets,” American Ceramic Society Bulletin, Vol. 72, pp. 93 98 (1993).
[2] Kulekci, M. K., “Processes and Apparatus Developments in Industrial Waterjet Applications,” International Journal of Machine Tools and Manufacture, Vol. 42, pp. 1297 1306 (2002).
[3] Liepmann, H. W., “Gas Kinetics and Gas Dynamics of Orifice Flow,” Journal of Fluid Mechanics, Vol. 10, pp. 65 79 (1961).
[4] Narasimha, R., “Orifice Flow at High Knudsen Numbers,” Journal of Fluid Mechanics, Vol. 10, pp. 371 384 (1961).
[5] Vahedi Tafreshi, H. and Pourdeyhimi, B., “The Effects of Nozzle Geometry on Waterjet Breakup at Hight Reynolds Numbers,” Experiments in Fluids, Vol. 35, pp. 364 371 (2003).
[6] Zheng, H. Y., Han, Z. Z., Chen, Z. D., Chen, W. L. and Yeo, S., “Quality and Cost Comparisons between Laser and Waterjet Cutting,” Journal of Materials Processing Technology, Vol. 62, pp. 294 298 (1996).
[7] Bach, Fr. W., Louis, H., Versemann, R. and Schenk, A., “Pure WJ Cleaning Process Characterization: Part II-Process Simulation,” Proceeding of the 8th International Conference on Management of Innovative Technologies, MIT’2005, pp. 15 21 (2005).
[8] Liu, H., Wang, J., Kelson, N. and Brown, R. J., “A Study of Abrasive Waterjet Characteristics by CFD Simulation,” Journal of Materials Processing Technologies, Vol. 153 154, pp. 488 493 (2004).
[9] Borutzky, W., Barnard, B. and Thoma, J., “An Orifice Flow Model for Laminar and Turbulent Conditions,” Simulation Modelling Practice and Theory, Vol. 10, pp. 141 152 (2002).
[10] Guo, Z., Ramulu, M. and Jenkins, M. G., “Analysis of the Waterjet Contact/Impact on Target Material,” Optics and Lasers in Engineering, Vol. 33, pp. 121 139 (2000).
[11] Bunnell, R. A., Heister, S. D., Yen, C. and Collicott, S. H., “Catitating Injector Flows: Validation of Nmerical Models and Simulations of Pressure Atomizers,” Atomization and Sprays, Vol. 9, pp.445 465 (1999).
[12] Charinrat, S. and Sakamon, D., “Numerical Simulation of Flow and Mixing Behavior of Impinging Streams of Shear-Thinning Fluids,” Ocean Engineering, Vol. 61, pp. 4884 4892 (2006).
[13] GarcÃÃa-Valladares, O., “Numerical Simulation of Trans-Critical Carbon Dioxide (R744) Flow through Short Tube Orifices,” Applied Thermal Engineering, Vol. 26, pp. 144 151 (2005).
[14] Ahn, K. H. and Ahn, J. H., “Numerical Simulation of Particle Motion through a Critical Orifice,” Journal of Aerosol Science, Vol. 29, pp. S833 S834 (1998).
[15] Adomian, G., “A Review of the Decomposition Method in Applied Mathematics,” Journal of Mathematical Analysis and Applications, Vol. 135, pp. 501 544 (1988).
[16] Bulut, H., Ergüt, M., Asil, V. and Bokor, R. H., “Numerical Solution of a Viscous Incompressible Flow Problem through an Orifice by Adomian Decomposition Method,” Applied Mathematics and Computation, Vol. 153, pp. 733 741 (2004).
[17] Almeida Medeiros, A. K., Lima, J. F., Medeiros, G. G., Silva Junior, N. F., Felipe, R. N. B. and Santos Felipe, R. C. T, “Parameters for Dimensional Inspection of Orifice Plates and Roughness of the Straight Stretches of the Tubing,” Brazilian Archives of Biology and Technology, Vol. 49, pp. 1 8 (2006).
[18] Launder, B. E. and Spalding, D. B., Lectures in Mathematical Models of Turbulence, Academic Press, London (1972). [19] John, H. O., “Abrasive Jet Mechanics,” March 8, 2005 thefabricator.com (2005).