Dynamic Responses of a Viscoelastic Material in Nanoscale by Using Harmonic Nanoindentation

Rwei-Ching  Chang; Bo-Chen  Huang

doi:10.6180/jase.2005.8.3.07

Dynamic Responses of a Viscoelastic Material in Nanoscale by Using Harmonic Nanoindentation

Rwei-Ching Chang This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Bo-Chen Huang¹

¹Department of Mechanical Engineering, St. John’s & St. Mary’s Institute of Technology, Taipei, Taiwan 251, R.O.C.

Received: January 8, 2005
Accepted: May 28, 2005
Publication Date: September 1, 2005

Download Citation: ||https://doi.org/10.6180/jase.2005.8.3.07

ABSTRACT

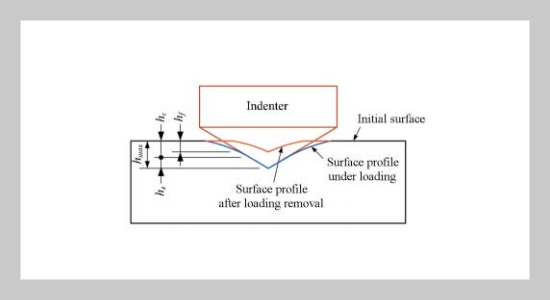
A rapid method to measure the viscoelastic properties of microstructures or nanocomposites is presented in this work. The time-dependent properties of viscoelastic materials in nanoscale are evaluated by using a harmonic nanoindentation test which is performed by a nanoindenter assembled on an atomic force microscope with a three sided pyramidal Berkovich probe tip. The experimental data are calculated by a numerical regression to fit the three-parameter Kelvin-Maxwell viscoelastic model and compared with the data determined from a creep test conducted by a tension machine. It shows that the compliances evaluated from the nanoindentation are smaller than those from the creep test, which means the properties evaluated by the nanoindentation are much stiffer than those by the creep test. Moreover, the relaxation time determined from the nanoindentation is smaller than the one from the creep test, meaning the response in the nanoindentation is quicker than the response in the creep test. The results present the variation of mechanical properties between the macro and micro scales.

Keywords: Nanoindentation, Dynamic Response, Viscoelasticity

REFERENCES

[1] Hertz, H., “Über Die Berührung Fester Elastischer Körper,” Journal Reine and Angewandte Mathematik, Vol. 92, pp. 156171 (1882).
[2] Boussinesq, J., Applications Des Potentials a L’etude De Equilibre Et Du Mouvement De Solides Elastiques, Gauthier-Villars, Paris, (1885).
[3] Sneddon, I. N., “The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile,” International Journal of Engineering Science, Vol. 3, pp. 4756 (1965).
[4] Oliver, W. C. and Pharr, G. M., “An Improved Technique for Determining Hardness and Elastic-modulus using Load and Displacement Sensing Indentation Experiments,” Journal of Materials Research, Vol. 7, pp. 1564
[5] Tabor, D., The Hardness of Metal, Oxford Univ. Press (1951).
[6] Bhushan, B., Handbook of Micro/Nanotribology, 2nd ed., CRC Press, Boca Raton (1999).
[7] Tabor, D., “Indentation Hardness: Fifty Years on a Personal View,” Philos. Mag. A, Vol. 74, pp. 12071221 (1996).
[8] Pharr, G. M., “Measurement of Mechanical Properties by Ultra-low Load Indentation,” Materials Science and Engineering, Vol. A253, pp.151159 (1998).
[9] Bhushan, B., Kulkarni, A. V., Bonin, W. and Wyrobek, J. T., “Nanoindentation and Picoindentation Measurements Using a Capacitive Transducer System in Atomic Force Microscopy,” Philos. Mag. A, Vol. 74, pp. 1117 1128 (1996).
[10] Bhushan, B., “Chemical, Mechanical and Tribological Characterization of Ultra-thin and Hard Amorphous Carbon Coatings as Thin as 3.5 nm: Recent Developments,” Diamond Related Materials, Vol. 8, pp. 19892015 (1999).
[11] Li, X., Diao, D. and Bhushan, B., “Fracture Mechanisms of Thin Amorphous Carbon Films in Nanoindentation,” Acta Mater., Vol. 45, pp. 44534461 (1997).
[12] Li, X. and Bhushan, B., “Measurement of Fracture Toughness of Ultra-thin Amorphous Carbon Films,” Thin Solis Films, Vol. 315, pp. 214221 (1998).
[13] Li, X. and Bhushan, B., “Evaluation of Fracture Toughness of Ultra-thin Amorphous Carbon Coatings Deposited by Different Deposition Techniques,” Thin Solis Films, Vol. 355, pp. 330336 (1999).
[14] Christensen, R. M., Theory of Viscoelasticity, An Introduction, 2nd ed., Academic Press, NY, U.S.A. (1982).
[15] Chung, T. J., Continuum Mechanics, Prentice-Hall, Inc., Englewood Cliffs, NJ, U.S.A. (1988).
[16] Nix, W. D. and Gao, H., “Indentation Size Effects in Crystalline Materials: A Law for Strain Gradient Plasticity,” Journal of Mechanics and Physics of Solids, Vol. 44, pp. 16211648 (1998).