Level-cut Approaches of First and Second Kind for Unique Solution Design in Fuzzy Engineering Optimization Problems

C. J. Shih; H. W. Lee

doi:10.6180/jase.2004.7.3.10

Level-cut Approaches of First and Second Kind for Unique Solution Design in Fuzzy Engineering Optimization Problems

C. J. Shih¹ and H. W. Lee This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Department of Mechanical and Electro-Mechanical Engineering Tamkang University, Tamsui, Taiwan 251, R.O.C

Received: January 12, 2004
Accepted: March 8, 2004
Publication Date: September 1, 2004

Download Citation: ||https://doi.org/10.6180/jase.2004.7.3.10

ABSTRACT

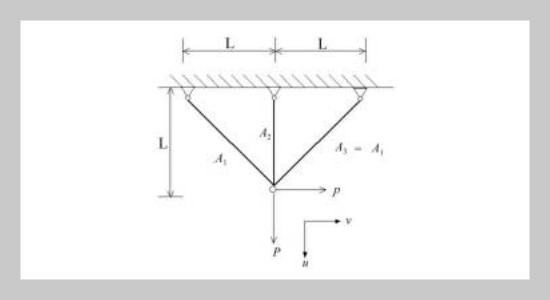
Two single level-cut approaches of the first and second kind for obtaining the unique compromise design in solving nonlinear optimum engineering design problems with fuzzy resources have been developed and presented in this paper. The conventional standard level-cuts method has been discussed for inspiring the proposed novel formulation consequently. The proposed strategies with the illustrative design examples indicate that the unique design as well as corresponding optimum level-cut value can be guaranteed obtained. Additionally, two wide-applicable linear or nonlinear membership functions of objective functions are presented depending on the practical situations of design tasks. The proposed level-cut approaches have been shown easy formulation and successfully employed to large-scaled structural design problems by sequential quadratic programming (SQP) technique combined with the finite element analysis.

Keywords: Level-cut Approach, Fuzzy Nonlinear Optimization, Engineering Design, Structural Optimization.

REFERENCES

[1] Zadeh, L. A., “Fuzzy Sets,” Information and Control, Vol. 8, pp. 338353 (1965).
[2] Zimmermann, H. J., “Applications of Fuzzy Sets Theory to Mathematical Programming,” Information Sciences, Vol. 36, pp. 2958 (1985).
[3] Wierzchon, S. T., “Linear Programming with Fuzzy Sets: A General Approach,” Mathematical Modeling, Vol. 9, pp. 447457 (1987).
[4] Leung, Y., Spatial analysis and planning under imprecision, North-Holland, Amsterdam (1988).
[5] Luhandjula, M. K., “Fuzzy Optimization an Appraisal,” Fuzzy Sets and Systems, Vol. 30, pp. 257282 (1989).
[6] Wang, G. Y. and Wang W. Q. “Fuzzy Optimum Design of Structures,” Engineering Optimization, Vol. 8, pp. 291300 (1985).
[7] Rao, S. S., “Description and Optimum Design of Fuzzy Mechanical Systems,” J. of Mechanisms, Transmissions, and Automation in Design, Vol. 109, pp. 126132 (1987).
[8] Rao, S. S., “Multiobjective Optimization of Fuzzy Structural Systems”, Int. J. for Numerical Methods in Engineering, Vol. 24, pp. 11571171 (1987).
[9] Rao, S. S. Sundararaju, K., Prakash, B. G. and Balakrishna, C., “Multiobjective Fuzzy Optimization Techniques for Engineering Design”, Computers & Structures, Vol. 42, pp. 3744 (1992).
[10] Yeh, Y. C. and Hsu, D. S., “Structural Optimization with Fuzzy Parameters,” Computers & Structures, Vol. 37, pp. 917924 (1990).
[11] Xu, C., “Fuzzy Optimization of Structures by The Two-phase Method,” Computers & Structures, Vol. 31, pp. 575580 (1989).
[12] Lai, Y. J. and Hwang, C. L., Fuzzy mathematical programming, Springer-Verlag, Berlin, pp. 7980 (1992).
[13] Verdegay, J. L., “Fuzzy Mathematical Programming,” In: Gupta, M. M. and Sanchez, E. Eds., Approximate reasoning in decision analysis, pp. 231236 (1982).
[14] Werner, B., “Interactive Fuzzy Programming Systems,” Fuzzy Sets and Systems, Vol. 23, pp. 131147 (1987).
[15] Zimmermamm, H. J., “Fuzzy Programming and Linear Programming with Several Objective Functions,” Fuzzy Sets and Systems, Vol. 1, pp. 45155 (1978).
[16] Bellman, R. E. and Zadeh, L. A., “Decision-making in a Fuzzy Environment,” Management Science, Vol. 17, B141B164 (1970).
[17] Rao, S. S., Engineering Optimization-Theory and Practice, 3rd edition, John Willy & Sons, Inc., New York, p. 112 (1996).
[18] Arakawa, M. and Yamakawa, H., “A Study on Optimum Design Using Fuzzy Numbers as Design Variables,” J. of JSME-C, 91-1001A, pp. 17101715 (1992).
[19] Hernandez, S. and Brebbia, C. A., Optimization of Structural Systems and Industrial Applications, Elsevier Applied Science, New York, pp. 9091 (1991).