Structurally Constrained H∞ Suboptimal Control Problems : Low-order Controller Design

Jaw-Kuen Shiau

doi:10.6180/jase.1999.2.4.03

Structurally Constrained H∞ Suboptimal Control Problems : Low-order Controller Design

Aerospace Engineering

Jaw-Kuen Shiau¹

¹Aerospace Engineering Department, Tamkang University Tamsui, Taiwan 25137, R.O.C.

Received: June 10, 1999
Accepted: January 25, 2000
Publication Date: January 25, 2000

Download Citation: ||https://doi.org/10.6180/jase.1999.2.4.03

ABSTRACT

This paper discusses a new iterative method for designing an H∞ low-order controller. The method is based on the optimization of a structurally constrained constant gain feedback controllers with linear matrix inequalities as the design constraints. In this new approach, the control gains are independent of any Riccati equation solutions. Controller constraints such as decentralization and positive realness can also be included in the design.

Keywords: Low-order controller, Linear matrix inequalities, H ∞ optimization

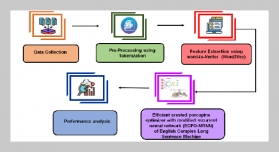
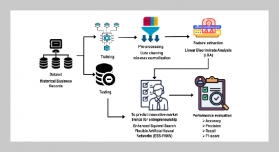
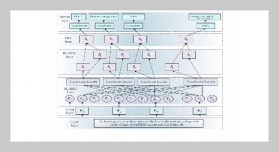
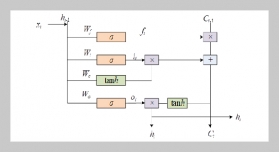
REFERENCES

[1] Boyd, S., Ghaoui, L. E., Feron, E. and Balakrishnan, V., Linear Matrix Inequalities in System and Control Theory, SIAM, Philadelphia, (1994).
[2] Davison, E. J. (ed.), "Benchmark Problems for Control System Design,'' Report of the IFAC Theory Committee, May, (1990).
[3] Doyle, J. C., Glover, K., Khargonekar, P. P., and Francis, B. A., "State-Space Solutions to Standard H2 and H ∞ Control Problems,'' IEEE Trans. Automat. Contr., Vol. 34, pp. 831-847, (1989).
[4] Edmunds, J. M., "Control System Design and Analysis using Closed-loop Nyquist and Bode Array," Int. J. Control, Vol. 30, No. 5, pp. 773-802, (1979).
[5] Gahinet, P. and Nemirovskii, A., LMI Lab: A Package for Manipulating and Solving LMI's, Version 2.0, (1993).
[6] Gahinet, P. and Ignat, A., "Low-Order H∞ Synthesis via LMIs,'' Proc., pp. 1499-1500, (1994).
[7] Gahinet, P. and Apkarian, P., "A Linear Matrix Inequality Approach to H∞ Control,'' Int. J. Robust and Nonlinear Control, Vol. 4, pp. 421-448, (1994).
[8] Geromel, J. C., Souza, C. C. de, and Skelton, R. E., "LMI Numerical Solutions for Output Feedback Stabilization,'' Proc., pp. 40-44. (1994).
[9] Ghaoui, L. E. and Balkrishnan, V., "Synthesis of Fixed-Structure Controllers via Numerical Optimization,'' Proc., pp. 2678-2683. (1994).
[10] Grigoriadis, K. M. and Skelton, R. E., "Fixed-Order Controller Problems Using Alternating Projection Methods,'' Proc., pp. 2003-2008. (1994).
[11] Goddard, P. J. and Glover, K., "Controller Reduction: Weights for Stability and Performance Preservation,'' Proceedings of the 32nd Conference on Decision and Control, pp. 2903-2908, San Antonio, Texas, December (1993).
[12] Goddard, P. J. and Glover, K., "Performance Preserving Frequency Weighted Controller Approximation: a Coprime Factorization Approach,'' Proceedings of the 33rd Conference on Decision and Control, Orlando, Florida, December (1994).
[13] Iwasaki, T. and Skelton, R. E., "All Controllers for the General H ∞ Control Problem: LMI Existence Conditions and State Space Formulas,'' Automatica, Vol. 30, pp. 1307-1317, (1994).
[14] Iwasaki, T. and Skelton, R. E., "A Unified Approach to Fixed Order Controller Design via Linear Matrix Inequalities,'' Proc., pp. 35-39, (1994).
[15] Kailath, T., Linear Systems, Prentice Hall, Inc., New Jersey, (1980).
[16] Khargonekar, P. P., Petersen, I. P., and Rotea, M. A., "H ∞ -Optimal Control with State-Feedback," IEEE Trans. Automat. Contr., Vol. AC-33, pp. 786-788, (1988).
[17] Lenz, K. E., Khargonekar, P. P., and Doyle, J. C., "Controller Order Reduction with Guaranteed Stability and Performance,'' Proc. American Control Conference, pp. 1697-1698. (1987).
[18] Mustafa, D. and Glover, K., "Controller Reduction by H ∞ -Balanced Truncation," IEEE Trans. Automat. Contr., Vol. AC-36, pp. 669-682, (1991).
[19] Shiau, J. K. and Chow, J. H., "Structurally Constrained H∞ Suboptimal Control Design Using an Iterative Linear Matrix Inequality Algorithm Based on a Dual Design Formulation," Tamkang Journal of Science and Engineering, Vol. 1, No. 2, pp. 133-143, (1998).
[20] Shiau, J. K., "Robust Decentralized Control: Model-Matching Formulation and Iterative Convex Programming Solutions," Ph.D. Thesis, Rensselaer Polytechnic Institute, December (1995).
[21] Taranto, G. N., "Robust Control Design for Power System Damping Controllers with Application to FACTS Devices," Ph.D. Thesis, Rensselaer Polytechnic Institute, December (1994).