Stress State And Pore Pressure Distribution Around A Horizontal Wellbore Within A Saturated Anisotropic Rock With Low Permeability

An Hai Nguyen

doi:10.6180/jase.202304_26(4).0014

Stress State And Pore Pressure Distribution Around A Horizontal Wellbore Within A Saturated Anisotropic Rock With Low Permeability

Material Engineering

An Hai Nguyen This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Petrovietnam Exploration Production Corporation - PVEP, Hanoi, Vietnam

Received: February 21, 2022
Accepted: May 17, 2022
Publication Date: July 29, 2022

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202304_26(4).0014

ABSTRACT

This study aims at deriving a closed-form solution of the effective stress state and pore pressure fields around a horizontal wellbore drilled in an anisotropic low permeable rock. As the rock is low permeable and the drilling rate is relatively fast, the undrained condition is thus reasonably assumed. A fully coupled hydro-mechanical problem under the undrained condition is shown to be equivalent to a purely mechanical one. The elastic fields of the latter one, including displacement, stress, and strain, around an elliptical-shaped borehole are derived by using the complex potential approach. Then, the elastic solution of the equivalent mechanical problem allows deriving the pore-elastic field of the considered hydro-mechanical problem. The presence of the pore pressure field solution exhibits the drilling-induced the over pore pressure and the depression around the borehole. This phenomenon was observed in situ when excavating the depth tunnel as reported in the literature. The comparison between the closed-form solution and the FEM solution is made to show the accuracy of the mathematical development. Parametric analysis is also done to study the effect of the anisotropic ratio (ratio of horizontal and vertical Young’s moduli) on the occurrence of over pore pressure and of depression. The presence of the poro-elastic closed-form solution derived in this study is very helpful for the borehole stability or the hydraulic fracturing design, in particular the probabilistic design.

Keywords: closed-form solution, fully hydro-mechanical coupling, horizontal well, anisotropy, overpressure, complex potential

REFERENCES

[1] Y. Feng and K. Gray, (2017) “Review of fundamental studies on lost circulation and wellbore strengthening" Journal of Petroleum Science and Engineering 152: 511–522. DOI: 10.1016/j.petrol.2017.01.052.
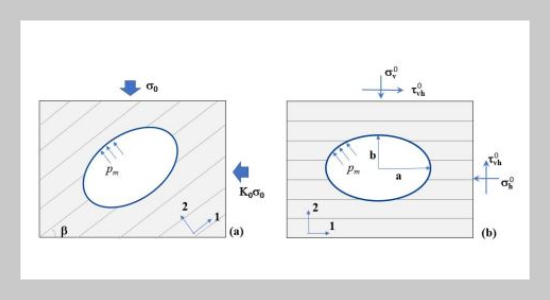
[2] D.-P. Do, N.-H. Tran, D. Hoxha, and H.-L. Dang, (2017) “Assessment of the influence of hydraulic and mechanical anisotropy on the fracture initiation pressure in permeable rocks using a complex potential approach" International Journal of Rock Mechanics and Mining Sciences 100: 108–123. DOI: 10.1016/j.ijrmms.2017.10.020.
[3] D.-P. Do, N.-H. Tran, H.-L. Dang, and D. Hoxha, (2019) “Closed-form solution of stress state and stability analysis of wellbore in anisotropic permeable rocks" International Journal of Rock Mechanics and Mining Sciences 113: 11–23. DOI: 10.1016/j.ijrmms.2018.11.002.
[4] S. G. Lekhnitskiih. Theory of elasticity of an anisotropic elastic body. Holden-day, 1963.
[5] Y. Li, G. Liu, J. Li, L. Yu, T. Zhang, and J. Lu, (2015) “Improving fracture initiation predictions of a horizontal wellbore in laminated anisotropy shales" Journal of Natural Gas Science and Engineering 24: 390–399. DOI: 10.1016/j.jngse.2015.04.002.
[6] T. Ma, Q. Zhang, P. Chen, C. Yang, and J. Zhao, (2017) “Fracture pressure model for inclined wells in layered formations with anisotropic rock strengths" Journal of Petroleum Science and Engineering 149: 393–408. DOI: 10.1016/j.petrol.2016.10.050.
[7] T. Ma, B. Wu, J. Fu, Q. Zhang, and P. Chen, (2017) “Fracture pressure prediction for layered formations with anisotropic rock strengths" Journal of Natural Gas Science and Engineering 38: 485–503. DOI: 10.1016/j.jngse.2017.01.002.
[8] V. Serajian. “A STUDY OF HYDRAULIC FRACTURE INITIATION IN TRANSVERSELY ISOTROPIC ROCKS". (phdthesis). Texas A&M University, 2011.
[9] A. E. Green and W. Zerna. Theoretical elasticity. Courier Corporation, 1992.
[10] J. C. Jaeger, N. G. Cook, and R. Zimmerman. Fundamentals of rock mechanics. JohnWiley & Sons, 2009.
[11] H. Chyanbin. Anisotropic Elastic Plates | SpringerLink. Springer, Boston, MA, 2010. Accessed: Feb. 19, 2022. URL: https://link.springer.com/book/10.1007/978-1-4419-5915-7.
[12] A. Stroh, (1962) “Steady state problems in anisotropic elasticity" Journal of Mathematics and Physics 41(1-4): 77–103. DOI: 10.1002/sapm196241177.
[13] B. S. Aadnoy, (1989) “Stresses around horizontal boreholes drilled in sedimentary rocks" Journal of Petroleum Science and Engineering 2(4): 349–360. DOI: 10.1016/0920-4105(89)90009-0.
[14] Y. Abousleiman and L. Cui, (1998) “Poroelastic solutions in transversely isotropic media for wellbore and cylinder" International Journal of Solids and Structures 35(34-35): 4905–4929. DOI: 10.1016/S0020-7683(98)00101-2.
[15] B. Amadei. Rock anisotropy and the theory of stress measurements. springer, 1983.
[16] H. Tran Manh, J. Sulem, and D. Subrin, (2015) “A closed-form solution for tunnels with arbitrary cross section excavated in elastic anisotropic ground" Rock Mechanics and Rock Engineering 48(1): 277–288. DOI: 10.1007/s00603-013-0542-0.
[17] J. Carter and J. Booker, (1982) “Elastic consolidation around a deep circular tunnel" International Journal of Solids and Structures 18(12): 1059–1074. DOI: 10.1016/0020-7683(82)90093-2.
[18] J. P. Carter and J. R. Booker, (1984) “Elastic consolidation around a lined circular tunnel" International journal of solids and structures 20(6): 589–608. DOI: 10.1016/0020-7683(84)90030-1.
[19] E. Detournay and A.-D. Cheng. “Poroelastic response of a borehole in a non-hydrostatic stress field”. In: International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 25. 3. Elsevier. 1988, 171–182. DOI: 10.1016/0148-9062(88)92299-1.
[20] C. Carranza-Torres and J. Zhao, (2009) “Analytical and numerical study of the effect of water pressure on the mechanical response of cylindrical lined tunnels in elastic and elasto-plastic porous media" International Journal of Rock Mechanics and Mining Sciences 46(3): 531–547. DOI: 10.1016/j.ijrmms.2008.09.009.
[21] A. Bobet, (2016) “Deep tunnel in transversely anisotropic rock with groundwater flow" Rock Mechanics and Rock Engineering 49(12): 4817–4832. DOI: 10.1007/s00603-016-1118-6.
[22] N. H. Tran. “Hydro-mechanical behavior of deep tunnels in anisotropic poroelastic medium". (phdthesis). University of Orleans, France, 2016.
[23] N.-H. Tran, D.-P. Do, and D. Hoxha, (2018) “A closedform hydro-mechanical solution for deep tunnels in elastic anisotropic rock" European Journal of Environmental and Civil Engineering 22(12): 1429–1445. DOI: 10.1080/19648189.2017.1285253.
[24] M. A. Biot, (1941) “General theory of three-dimensional consolidation" Journal of applied physics 12(2): 155–164. DOI: 0.1063/1.1712886.
[25] O. Coussy. Poromechanics. John Wiley & Sons, 2004.
[26] M.-N. Vu, L. M. Guayacán Carrillo, and G. Armand, (2020) “Excavation induced over pore pressure around drifts in the Callovo-Oxfordian claystone" European Journal of Environmental and Civil Engineering: 1–16. DOI: 10.1080/19648189.2020.1784800.
[27] F. Bumbieler, C. Plúa, S. Tourchi, M.-N. Vu, J. Vaunat, A. Gens, and G. Armand, (2021) “Feasibility of constructing a full-scale radioactive high-level waste disposal cell and characterization of its thermo-hydro-mechanical behavior" International Journal of Rock Mechanics and Mining Sciences 137: 104555. DOI: 10.1016/j.ijrmms.2020.104555.
[28] S. Tourchi, J. Vaunat, A. Gens, F. Bumbieler, M.-N. Vu, and G. Armand, (2021) “A full-scale in situ heating test in Callovo-Oxfordian claystone: observations, analysis and interpretation" Computers and Geotechnics 133: 104045. DOI: 10.1016/j.compgeo.2021.104045.
[29] N. Conil, M. Vitel, C. Plua, M. N. Vu, D. Seyedi, and G. Armand, (2020) “In situ investigation of the THM behavior of the Callovo-Oxfordian claystone" Rock Mechanics and Rock Engineering 53(6): 2747–2769. DOI: 10.1007/s00603-020-02073-8.
[30] Z. Yu, J. Shao, G. Duveau, M.-N. Vu, and G. Armand, (2021) “Numerical modeling of deformation and damage around underground excavation by phase-field method with hydromechanical coupling" Computers and Geotechnics 138: 104369. DOI: 10.1016/j.compgeo.2021.104369.
[31] M. A. Mánica, A. Gens, J. Vaunat, G. Armand, and M.-N. Vu, (2021) “Numerical simulation of underground excavations in an indurated clay using non-local regularisation. Part 1: formulation and base case" Géotechnique: 1–21. DOI: 10.1680/jgeot.20.P.246.
[32] H. X. Han, S. Yin, and B. S. Aadnoy, (2018) “Impact of elliptical boreholes on in situ stress estimation from leak-off test data" Petroleum Science 15(4): 794–800. DOI: 10.1007/s12182-018-0248-8.
[33] N.-T. Tran, D.-P. Do, D. Hoxha, M.-N. Vu, and G. Armand, (2021) “Kriging-based reliability analysis of the long-term stability of a deep drift constructed in the Callovo-Oxfordian claystone" Journal of Rock Mechanics and Geotechnical Engineering 13(5): 1033–1046. DOI: 10.1016/j.jrmge.2021.06.009.
[34] D.-P. Do, M.-N. Vu, N.-T. Tran, and G. Armand, (2021) “Closed-Form Solution and Reliability Analysis of Deep Tunnel Supported by a Concrete Liner and a Covered Compressible Layer Within the Viscoelastic Burger Rock" Rock Mechanics and Rock Engineering 54(5): 2311–2334. DOI: 10.1007/s00603-021-02401-6.
[35] N. H. Tran, D. P. Do, M. N. Vu, T. T. N. Nguyen, D. T. Pham, and H. T. Trieu, (2022) “Combined effect of anisotropy and uncertainty on the safe mud pressure window of horizontal wellbore drilled in anisotropic saturated rock" International Journal of Rock Mechanics and Mining Sciences 152: 105061. DOI: 10.1016/j.ijrmms.2022.10506.
[36] C. Plúa, M.-N. Vu, D. M. Seyedi, and G. Armand, (2021) “Effects of inherent spatial variability of rock properties on the thermo-hydro-mechanical responses of a highlevel radioactive waste repository" International Journal of Rock Mechanics and Mining Sciences 145: 104682. DOI: 10.1016/j.ijrmms.2021.104682.
[37] C. Plua, M. Vu, G. Armand, J. Rutqvist, J. Birkholzer, H. Xu, R. Guo, K. Thatcher, A. Bond, W. Wang, et al., (2021) “A reliable numerical analysis for large-scale modelling of a high-level radioactive waste repository in the Callovo-Oxfordian claystone" International Journal of Rock Mechanics and Mining Sciences 140: 104574. DOI: 10.1016/j.ijrmms.2020.104574.
[38] M.-N. Vu, G. Armand, and C. Plua, (2020) “Thermal pressurization coefficient of anisotropic elastic porous media" Rock Mechanics and Rock Engineering 53(4): 2027–2031. DOI: 10.1007/s00603-019-02021-1.
[39] Code Aster. URL: https://www.code-aster.org/spip.php?rubrique2.