Explicit Finite Difference Approximation Method for Solving the Riesz Space Fractional Percolation Equation

Iman I. Gorial

doi:10.6180/jase.202112_24(6).0020

Explicit Finite Difference Approximation Method for Solving the Riesz Space Fractional Percolation Equation

Material Engineering

Iman I. Gorial This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Department of Materials Engineering, University of Technology, Iraq

Received: December 21, 2020
Accepted: May 10, 2021
Publication Date: June 30, 2021

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202112_24(6).0020

ABSTRACT

This paper presents an efficient approximation method for solving the Riesz space fractional percolation equation mixed fractional derivative (RSFPEMFD) with the initial condition (IC) and derivative boundary conditions (DBC) using explicit finite difference method (EFDM). The shifted Grunwald estimate was used for analysis of the mixed fractional derivatives. In addition, the analysis method of consistency, stability, and convergence was used for analyzing the EFDM. To demonstrate the efficiency and validity of the proposed algorithm, some illustrative examples are given and comparing results with the exact solution. The results are displayed when necessary in tables using the MathCAD and MATLAB software package. The EFDM for solving RSFPEMFD has been demonstrated to be effective and reliable.

Keywords: Explicit finite difference method (EFD), Fractional percolation equation (FPE), Riesz mixed fractional derivative, Stability, Convergence of numerical method

REFERENCES

[1] S. Noeiaghdam and E. K. Ghiasi. An efficient method to solve the mathematical model of HIV infection for CD8+ T-cells. 2019. arXiv: 1907.01106.
[2] P. A. Naik, J. Zu, and K. M. Owolabi, (2020) “Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order" Physica A: Statistical Mechanics and its Applications 545: DOI: 10 . 1016/j .physa. 2019 .123816.
[3] P. A. Naik, J. Zu, and K. M. Owolabi, (2020) “Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control" Chaos, Solitons and Fractals 138: DOI: 10.1016/j.chaos.2020.109826.
[4] P. A. Naik, (2020) “Global dynamics of a fractionalorderSIR epidemic model with memory" International Journal of Biomathematics 13(8): DOI: 10 . 1142 /S1793524520500710.
[5] J. Singh, D. Kumar, Z. Hammouch, and A. Atangana, (2018) “A fractional epidemiological model for computer viruses pertaining to a new fractional derivative" Applied Mathematics and Computation 316: 504–515. DOI: 10.1016/j.amc.2017.08.048.
[6] D. Sidorov, I. Muftahov, N. Tomin, D. Karamov, D. Panasetsky, A. Dreglea, F. Liu, and A. Foley. A dynamic analysis of energy storage with renewable and diesel generation using volterra equations. 2019.
[7] Q. Wang, J. Ma, S. Yu, and L. Tan, (2020) “Noise detection and image denoising based on fractional calculus" Chaos, Solitons and Fractals 131: DOI: 10.1016/j . chaos.2019.109463.
[8] T. Chen and D. Wang, (2020) “Combined application of blockchain technology in fractional calculus model of supply chain financial system" Chaos, Solitons and Fractals 131: DOI: 10.1016/j.chaos.2019.109461.
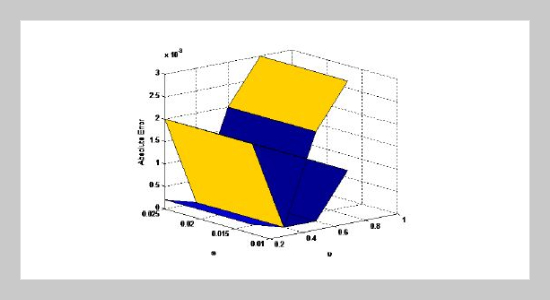
[9] Q. Zhang, N. Cui, Y. Li, B. Duan, and C. Zhang, (2020) “Fractional calculus based modeling of open circuit voltage of lithium-ion batteries for electric vehicles" Journal of Energy Storage 27: DOI: 10.1016/j.est.2019.100945. Fig. 12. The absolute error the numerical and exact solutions at g=0.7, h=0.8.
[10] P. De Angelis, R. De Marchis, A. L. Martire, and I. Oliva, (2020) “A mean-value Approach to solve fractional differential and integral equations" Chaos, Solitons and Fractals 138: DOI: 10.1016/j.chaos.2020. 109895.
[11] A. I. Akimov, E. O. Karakulina, I. A. Akimov, and V. V. Tugov, (2018) “Mathematical models of heat exchange in multilayer constructions with various thermalphysic characteristics in industrial installations" International Review on Modelling and Simulations 11(2): 59–66. DOI: 10.15866/iremos.v11i2.13904.
[12] M. H. Alrashdan, (2020) “Quality and damping factors optimization using taguchi methods in cantilever beam based piezoelectric micro-power generator for cardiac pacemaker applications" International Review on Modelling and Simulations 13(2): 74–84. DOI: 10.15866/iremos.v13i2.18347.
[13] N. Petford and M. A. Koenders. Seepage flow and consolidation in a deforming porous medium.
[14] S. Chen, F. Liu, I. Turner, and V. Anh, (2013) “An implicit numerical method for the two-dimensional fractional percolation equation" Applied Mathematics and Computation 219(9): 4322–4331. DOI: 10.1016/j.amc.2012.10.003.
[15] S. Chen, F. Liu, I. Turner, and V. Anh, (2013) “An implicit numerical method for the two-dimensional fractional percolation equation" Applied Mathematics and Computation 219(9): 4322–4331. DOI: 10.1016/j.amc.2012.10.003.
[16] S. Chen, F. Liu, and V. Anh, (2011) “A novel implicit finite difference method for the one-dimensional fractional percolation equation" Numerical Algorithms 56(4):517–535. DOI: 10.1007/s11075-010-9402-0.
[17] F. Liu, P. Zhuang, V. Anh, I. Turner, and K. Burrage, (2007) “Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation" Applied Mathematics and Computation 191(1): 12–20. DOI: 10.1016/j.amc.2006.08.162.
[18] Y. M. Chen, Y. Q. Wei, D. Y. Liu, and H. Yu, (2015) “Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets" Applied Mathematics Letters 46: 83–88. DOI: 10 .1016/j.aml.2015.02.010.
[19] S. Shen, F. Liu, V. Anh, I. Turner, and J. Chen, (2013) “A characteristic difference method for the variable-order fractional advection-diffusion equation" Journal of Applied Mathematics and Computing 42(1-2): 371–386. DOI: 10.1007/s12190-012-0642-0.
[20] X. Zhao, Z. zhong Sun, and G. E. Karniadakis, (2015) “Second-order approximations for variable order fractional derivatives: Algorithms and applications" Journal of Computational Physics 293: 184–200. DOI: 10.1016/ j.jcp.2014.08.015.
[21] Q. Liu and F. Liu, (2009) “Modified alternating direction methods for solving a two-dimensional non-continuous seepage flow with fractional derivatives" Mathematica Numerica Sinica 31(2): 179–194.
[22] S. Chen, F. Liu, and K. Burrage, (2014) “Numerical simulation of a new two-dimensional variable-order fractional percolation equation in non-homogeneous porous media" Computers and Mathematics with Applications 68(12): 2133–2141. DOI: 10.1016/j.camwa.2013. 01.023.
[23] B. Guo, Q. Xu, and Z. Yin, (2016) “Implicit finite difference method for fractional percolation equation with Dirichlet and fractional boundary conditions" Applied Mathematics and Mechanics (English Edition) 37(3): 403–416. DOI: 10.1007/s10483-016-2036- 6.
[24] R. Lin, F. Liu, V. Anh, and I. Turner, (2009) “Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation" Applied Mathematics and Computation 212(2): 435–445. DOI: 10.1016/j.amc.2009.02.047.
[25] S. B. Yuste and L. Acedo, (2005) “An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations" SIAM Journal on Numerical Analysis 42(5): 1862–1874. DOI: 10.1137/030602666.
[26] O. González-Gaxiola, A. Biswas, M. Asma, and A. K. Alzahrani, (2020) “Optical Dromions and DomainWalls with the Kundu – Mukherjee – Naskar Equation by the Laplace – Adomian Decomposition Scheme" Regular and Chaotic Dynamics 25(4): 338–348. DOI: 10.1134/ S1560354720040036.
[27] O. González-Gaxiola, A. Biswas, M. Asma, and A. K. Alzahrani, (2021) “Highly dispersive optical solitons with non-local law of refractive index by Laplace-Adomian decomposition" Optical and Quantum Electronics 53(1): DOI: 10.1007/s11082-020-02679-w.
[28] K. Hosseini, M. Ilie, M. Mirzazadeh, and D. Baleanu, (2020) “A detailed study on a new (2 + 1) -dimensional mKdV equation involving the Caputo–Fabrizio timefractional derivative" Advances in Difference Equations 2020(1): DOI: 10.1186/s13662-020-02789-5.
[29] P. Kamal, F. Liu, Y. Yan, and G. Roberts. “Finite difference method for two-sided space-fractional partial differential equations”. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). 9045. Springer Verlag, 2015, 307–314. DOI: 10.1007/978-3-319-20239-6_33.
[30] L. Su, W. Wang, and Z. Yang, (2009) “Finite difference approximations for the fractional advection-diffusion equation" Physics Letters, Section A: General, Atomic and Solid State Physics 373(48): 4405–4408. DOI: 10. 1016/j.physleta.2009.10.004.
[31] C. Tadjeran, M. M. Meerschaert, and H. P. Scheffler, (2006) “A second-order accurate numerical approximation for the fractional diffusion equation" Journal of Computational Physics 213(1): 205–213. DOI: 10.1016/j. jcp.2005.08.008.