Hydromagnetic Flow of a Conducting Micropolar Fluid over a Plane Wall with Heat Transfer

Hazem A.  Attia; Karem M.  Ewis

doi:10.6180/jase.2011.14.1.01

Hydromagnetic Flow of a Conducting Micropolar Fluid over a Plane Wall with Heat Transfer

Hazem A. Attia This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Karem M. Ewis¹

¹Department of Engineering Mathematics and Physics, Faculty of Engineering, Fayoum University, Fayoum, Egypt

Received: May 2, 2006
Accepted: July 12, 2006
Publication Date: March 1, 2011

Download Citation: ||https://doi.org/10.6180/jase.2011.14.1.01

ABSTRACT

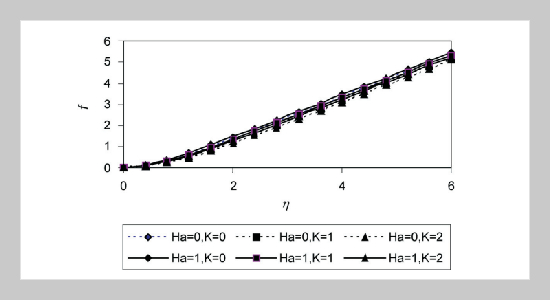
The steady hydromagnetic laminar flow of an incompressible non-Newtonian micropolar fluid impinging on a plane wall with heat transfer is investigated. A uniform magnetic field is applied normal to the plate which is maintained at a constant temperature. Numerical solution for the governing nonlinear momentum and energy equations is obtained. The effect of the uniform magnetic field and the characteristics of the non-Newtonian fluid on both the flow and heat transfer is presented and discussed.

Keywords: Stagnation Point Flow, Non-Newtonian Fluid, Magnetic Field, Numerical Solution, Heat Transfer

REFERENCES

[1] Hiemenz, K., Dingler Polytech. J., Vol. 326, p. 321 (1911).
[2] Homann, F. and Angew, Z., Math. Mech., Vol. 16, p. 153 (1936).
[3] Schlichting, H. and Bussmann, K., Schri. Dtsch. Akad. Luftfahrtforschung, Ser. B, Vol. 7, p. 25 (1943).
[4] Preston, J. H., Reports and Memoirs, British Aerospace Research Council, London, No. 2244 (1946).
[5] Ariel, P. D., J. Appl. Mech., Vol. 61, p. 976 (1994).
[6] Weidman, P. D. and Mahalingam, S., J. Engg. Math., Vol. 31, p. 305 (1997).
[7] Na, T. Y., Computational Methods in Engineering Boundary Value Problem, Academic Press, New York, p. 107 (1979).
[8] Ariel, P. D., Acta Mech., Vol. 103, p. 31 (1994).
[9] Attia, H. A., Arab. J. Sci. Engg., Vol. 28, p. 107 (2003).
[10] Attia, H. A., Can. J. Phys., Vol. 81, p. 1223 (2003).
[11] Massoudi, M. and Ramezan, M., ASME HTD, Vol. 130, p. 81 (1990).
[12] Massoudi, M. and Ramezan, M., Mech. Res. Commun., Vol. 19, p. 129 (1992).
[13] Garg, V. K., Acta Mech., Vol. 104, p. 159 (1994).
[14] Rajeshwari, G. K. and Rathna, S. L. and Angew, Z., Math. Phys., Vol. 13, p. 43 (1962).
[15] Beard, D. W. and Walters, K., Proc. Cambridge Philos. Soc., Vol. 14, p. 757 (1992).
[16] Teipel, I., Rheological Acta., Vol. 25, p. 75 (1986).
[17] Ariel, P., D., International J. Numerical Methods Fluids., Vol. 14, p. 757 (1992).
[18] Djukic, D. S., ASME J. Appl. Mech., Vol. 40, p. 822 (1974).
[19] Teipel, I., CSME Trans., Vol. 12, p. 57 (1988).
[20] Ariel, P. D., J. Comput. Appl. Math., Vol. 59, p. 9 (1995).
[21] Attia, H. A., Can. J. Phys., Vol. 78, p. 875 (2000).
[22] Nath, G., Rheological Acta, Vol. 14, p. 850 (1975).
[23] Nazar, R., Amin, N., Filip, D. and Pop, I., International J. of Non-Linear Mechanics, Vol. 39, p. 1227 (2004).
[24] Sutton, G. W. and Sherman, A., Engineering Magnetohydrodynamics, McGraw-Hill, New York (1965).