Rajneesh Kumar This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Leena Rani²

¹Department of Mathematics, Kurukshetra University, Kurukshetra 136119 Haryana, India
²M. M. Engineering College, Kurukshetra University, Mullana (Ambala) 133203, Haryana, India

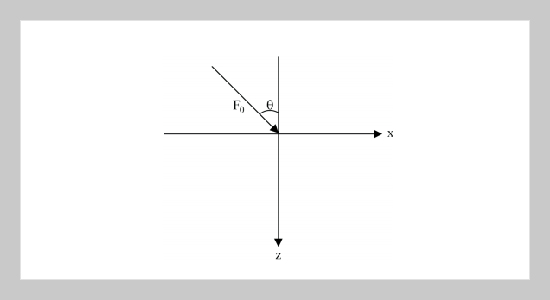
REFERENCES

1. [1] Chadwick, P., Thermoelasticity, the Dynamic Theory, Progress in Solid Mechanics, Vol. 1 (Sneddon, I. N., Hill. R., eds.), p. 265, Amsterdam: North-Holland (1960).
2. [2] Lord, H. W. and Shulman, Y., “AGeneralized Dynamical Theory of Thermoelasticity,” J. Mech. Phys. Solids, Vol. 15, pp. 299
   309 (1967).
3. [3] Green, A. E. and Lindsay, K. A., “Thermoelasticity,” J. Elasticity, Vol. 2, pp. 1
   7 (1972).
4. [4] Chandrasekharaiah, D. S., “Thermoelasticity with Second Sound: A Review,” Appl. Mech. Rev. Vol. 39, pp. 355
   376 (1986).
5. [5] Ignaczak, J., Generalized Thermoelasticity and its Applications. In: Thermal stresses, Vol. III (Hetnarski, R. B. ed.). Chapter 4. Oxford: Elsevier (1989).
6. [6] Joseph, D. D. and Preziosi, L., “Heat Waves,” Revs. Mod. Phys. Vol. 61, pp. 41
   73 (1989) and addendum Vol. 62, pp. 375
   391 (1990).
7. [7] Green, A. E. and Naghdi, P. M., “A Re-Examination of the Basic Postulates of Thermomechanics,” Proc. R. Soc. London, Ser. A, Vol. 432, pp. 171
   194 (1991).
8. [8] Green, A. E. and Naghdi, P. M., “On Undamed Heat Waves in Elastic Solid,” J. Thermal Stresses, Vol. 15, pp. 253
   264 (1992).
9. [9] Green, A. E. and Naghdi, P. M., “Thermoelasticity without Energy Dissipation,” J. Elasticity, Vol. 31, pp. 189
   208 (1993).
10. [10] Green, A. E. and Naghdi, P. M., “A Unified Procedure for Construction of Theories of Deformable Media. I. Classical Continuum Physics, II. Generalized Continua, III. Mixtures of Interacting Continua,” Proc. R. Soc. London A, Vol. 448, pp. 335
    356, 357
    377, 379
    388 (1995).
11. [11] Chandrasekharaiah, D. S., “A Note on the Uniqueness of Solution in the Linear Theory of Thermoelasticity without Energy Dissipation,” J. Elasticity, Vol. 43, pp. 279
    283 (1996).
12. [12] Chandrasekharaiah, D. S., “A Uniqueness Theorem in the Theory of Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 19, pp. 267
    272 (1996).
13. [13] Li, H. and Dhaliwal, R. S., “Thermal Shock Problem in Thermoelasticity without Energy Dissipation,” Indian J. pure appl. Math., Vol. 27, pp. 85
    101 (1996).
14. [14] Scott, N. H., “Energy and Dissipation of Inhomogeneous Plane Waves in Thermoelasticity,” Wave motion, Vol. 23, pp. 393
    406 (1996).
15. [15] Chandrasekharaiah, D. S. and Srinath, K. S., “Axisymmetric Thermoelastic Interaction without Energy Dissipation in an Unbounded Body with Cylindrical Cavity,” J. Elasticity, Vol. 46, pp. 19
    31 (1997).
16. [16] Chandrasekharaiah, D. S. and Srinath, K. S., “Thermoelastic Waves without Energy Dissipation in an Unbounded Body with Spherical Cavity,” Internat. J. Math and Math. Sci., Vol. 23, pp. 555
    562 (2000).
17. [17] Iesan, D., “On the Theory of Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 21, pp. 295
    307 (1998).
18. [18] Quintanilla, R., “On the Spatial Behaviour in Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 22, pp. 213
    224 (1999).
19. [19] Quintanilla, R., “Instability, Non-existence in the Nonlinear Theory of Thermoelasticity without Energy Dissipation,” Continuum Mech. Thermodyn., Vol. 13, pp. 121
    129 (2001).
20. [20] Quintanilla, R., “On Existence in Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 25, pp. 195
    202 (2002).
21. [21] Wang, J. and Slattery, S. P., “Thermoelasticity without Energy Dissipation for Initially Stressed Bodies,” International Journal of Mathematics and Mathematical Sciences, Vol. 31, pp. 329
    337 (2002).
22. [22] Quintanilla, R., “Thermoelasticity without Energy Dissipation of Nonsimple Materials.” Jour. Appl. Mathematics Mechanics (ZAMM), Vol. 83, pp. 172
    180 (2003).
23. [23] Love, A. E. H., A Treatise on the Mathematical Theory of Elasticity, Dover Publications, New York, U.S.A. (1944).
24. [24] Maruyama, T., “On Two-Dimensional Elastic Dislocations in an Infinite and Semi-Infinite Medium,” Bull. Earthq. Res. Inst. Vol. 44, pp. 811
    871 (1966).
25. [25] Okada, Y., “Surface Deformation due to Inclined Shear and Tensile Faults in a Homogeneous Isotropic HalfSpace,” Bull. Seismol. Soc. Am. Vol. 75, pp. 1135
    1154 (1985).
26. [26] Okada, Y., “Internal Deformation due to Shear and Tensile Faults in a Half-Space,” Bull. Seismol. Soc. Am. Vol. 82, pp. 1018
    1040 (1992).
27. [27] Kuo, J. T., “Static Response of a Multilayered Medium under Inclined Surface Loads,” Journal of Geophysical research, Vol. 74, pp. 3195
    3207 (1969).
28. [28] Gerstle, F. P. and Pearsall, G. W., “The Stress Response of an Elastic Surface to a High Velocity, Unlubricated Punch,” ASME Jounal of Applied Mechanics, Vol. 41, pp. 1036
    1040 (1974).
29. [29] Kumar, R., Miglani, A. and Garg, N. R., “Plane Strain Problem of Poroelasticity using Eigenvalue Approach,” Proceeding Indian Acad. Sci. (Earth Planet Sci.), Vol. 109, pp. 371
    380 (2000).
30. [30] Kumar, R., Miglani, A. and Garg, N. R., “Response of an Anisotropic Liquid-Saturated Porous Medium due to Two-Dimensional Sources,” Proceeding Indian Acad. Sci. (Earth Planet Sci.), Vol. 111, pp. 143
    151 (2002).
31. [31] Kumar, R. and Rani, L., “Response of Thermoelastic Half-Space with Voids due to Inclined Load,” (Accepted for publication in International Journal of Applied Mechanics and Engineering, IJAME, POLAND).
32. [32] Kumar, R. and Rani, L., “Deformation due to Inclined Load in Thermoelastic Half-Space with Voids,” Archives of Mechanics, POLAND, Vol. 57, pp. 7
    24 (2005)
33. [33] Honig, G. and Hirdes, U., “A Method for the Numerical Inversion of Laplace Transform,” Journal of Computational and Applied Mathematics, Vol. 10, pp. 113
    132 (1984).
34. [34] Press,W. H., Teukolshy, S. A., Vellerling, W. T. and Flannery, B. P., Numerical Recipes in FORTRAN (2nd edn.), Cambridge University Press, Cambridge (1986).
35. [35] Dhaliwal, R. S. and Singh, A., Dynamic Coupled Thermoelasticity, p. 726, Hindustan Publ. Corp., New Delhi, India (1980).