Hazem Ali Attia This email address is being protected from spambots. You need JavaScript enabled to view it.1 and Mohamed Eissa Sayed-Ahmed2 1Department of Mathematics, College of Science, Al-Qasseem University, P.O. Box 237, Buraidah 81999, KSA
2Department of Engineering Mathematics and Physics, Faculty of Engineering, Cairo University (El-Fayoum Branch), Egypt
Received:
March 4, 2005
Accepted:
September 12, 2005
Publication Date:
September 1, 2006
Download Citation:
||https://doi.org/10.6180/jase.2006.9.3.02
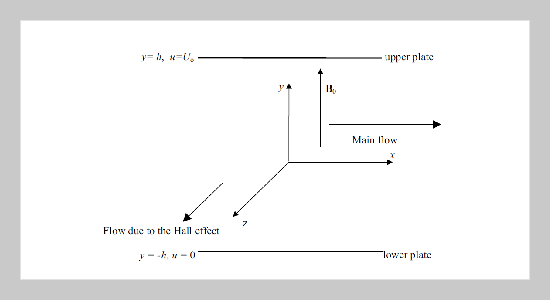
The transient hydromagnetic impulsively Lid-Driven flow of an electrically, conducting, viscous, incompressible, and non-Newtonian Casson fluid bounded by two parallel non-conducting plates is studied with heat transfer considering the Hall effect. An external uniform magnetic field is applied perpendicular to the plates and the fluid motion is subjected to a pressure gradient in the axial direction. The lower plate is stationary and the upper plate is suddenly set into motion and simultaneously suddenly isothermally heated to a temperature other than the lower plate temperature. Numerical solutions are obtained for the governing momentum and energy equations taking the Joule and viscous dissipations into consideration. The effect of the Hall term and the parameter describing the non-Newtonian behavior on both the velocity and temperature distributions are studied.ABSTRACT
Keywords:
Lid-driven Flow, Hydromagneticflow, Heard Transfer, Finite Differences
REFERENCES