Dynamic Stiffness Matrices for Linear Members with Distributed Mass

Chih-Peng Yu; Jose M. Roesset

doi:10.6180/jase.2001.4.4.04

Dynamic Stiffness Matrices for Linear Members with Distributed Mass

Chih-Peng Yu This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Jose M. Roesset This email address is being protected from spambots. You need JavaScript enabled to view it.²

¹Department of Construction Engineering Chaoyang University of Technology Wufeng, Taichung 413, Taiwan
²Department of Civil Engineering Texas A&M University College Station, TX 77843, U.S.A.

Received: April 1, 2001
Accepted: June 13, 2001
Publication Date: December 1, 2001

Download Citation: ||https://doi.org/10.6180/jase.2001.4.4.04

ABSTRACT

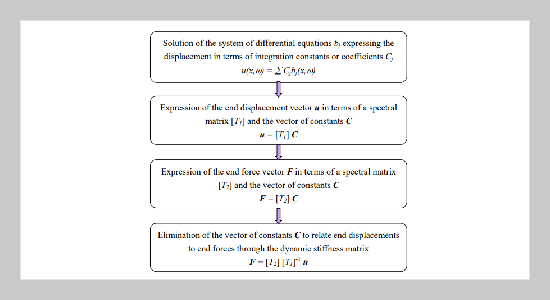
The analytical determination of dynamic stiffness matrices in the frequency domain for linear structural members with distributed mass provides an efficient and accurate procedure for the dynamic analysis of frames. This formulation allows to account not only for the distributed masses but also for wave propagation effects within each member. It provides therefore a more economical solution and a more accurate one than the use of lumped or even consistent mass matrices, which would require dividing the member into various elements to reproduce these effects, particularly for high frequencies. This problem has been discussed recently in relation to the seismic analysis of structures (bridge piers in particular) subjected to vertical ground accelerations. It had always been a major consideration in the interpretation of dynamic non-destructive tests based on impact loads and wave propagation. In this paper the dynamic stiffness matrices for linear members with different formulations are presented together.

Keywords: Dynamic Stiffness, Frequency Domain Solution, Continuous Formulation

REFERENCES

[1] Banerjee, J. R. and William, F. W.," Exact Bernoulli-Euler Dynamic Stiffness Matrix for a Range of Tapered Beams," International Journal for Numerical Methods in Engineering, Vol. 21, pp. 2289-2302 (1985).
[2] Banerjee, J. R. and William, F. W., " An exact dynamic stiffness matrix for coupled extentional-torsional vibration of structural members ", Computers and Structures, Vol. 50, pp. 161-166 (1994).
[3] Banerjee, J. R. and William, F. W.," Coupled bending-torsional dynamic stiffness matrix for an axially loaded timoshenko beam elements", International Journal of Solids and Structures, Vol. 31, pp. 749-762 (1994).
[4] Chen, Y.-H. and Sheu, J.-T., " Axial loaded damped timoshenko beam on viscoelastic foundation", Int. J. for Numerical Methods in Engineering, Vol. 36, pp. 1013-1027 (1993).
[5] Chen, Y.-H. and Sheu, J.-T., " Beam length and dynamic stiffness", International Computer Methods in Applied Mechanics and Engineering, Vol. 129, pp. 311-318 (1996).
[6] Doyle, J. F., Wave Propagation in Structures - An FFT-Based Spectral Analysis Methodology, Springer-Verlay (1989).
[7] Doyle, J. F., Wave Propagation in Structures - Spectral Analysis Using Fast Discrete Fourier Transform, Springer-Verlay, 2nd. Ed. (1997).
[8] Gopalakrishnan, S. and Doyle, J. F., " Wave propagation in connected waveguides of varying cross-section ", Journal of Sound and Vibration, Vol. 175, pp. 374-363 (1994).
[9] Graff, K. F., Wave Motion in Elastic Solids, Dover, U. S. A. (1975).
[10] Koloušek, V., Dynamics in Engineering Structures, Butterworths, London (1973).
[11] Latona, R. W. "Analysis of Building Frames for Natural Frequencies and Natural Mode Shapes," Inter American Program, Civil Engineering Department, MIT (1969).
[12] Martin, M., Gopalakrishnan, S., and Doyle, J. F., " Wave Propagation in Multiply Connected Deep Waveguides ", Journal of Sound and Vibration, Vol. 174, pp. 521-538 (1993).
[13] Mindlin, R. D. and Herrmann, G., " A One-Dimensional Theory of Compressional Waves in an Elastic Rod," Proceedings of the First U.S. National Congress of Applied Mechanics, pp. 187-191 (1951).
[14] Novak, M., "Dynamic Stiffness and Damping of Piles", Canadian Geotechnical Journal, Vol. 2, pp. 574-598 (1974).
[15] Papaleontiou, C. G., "Dynamic Analysis of Building Structures under Combined Horizontal and Vertical Vibrations," Doctoral Dissertation, University of Texas at Austin (1992).
[16] Sanchez-Salinero, I., "Static and Dynamic Stiffnesses of Single Piles," Department of Civil Engineering, The University of Texas at Austin, Geotechnical Engineering Report GR82-31 (1982).
[17] Yu, C. P., "Determination of Pile Lengths Using Flexural Waves," Civil Engineering Department, The University of Texas at Austin, Report GR95-3, Geotechnical Engineering Center (1995).
[18] Yu, C. P., "Effect of Vertical Earthquake Components on Bridge Responses," Doctoral Dissertation, University of Texas at Austin, TX, U. S. A. (1996).
[19] Yu, C. P. and Roësset, J. M., "Dynamic Analysis of Structures Using Continuous Solutions in Frequency Domain," Proceedings of EASEC-6 Conference on Structural Engineering & Construction, Taipei, Taiwan, Vol.2, pp 1369-1375 (1998).