Optimal Mechanical Design with Robust Performance by Fuzzy Formulation Strategy

C.J. Shih; T.J. Tseng

doi:10.6180/jase.2001.4.1.07

Optimal Mechanical Design with Robust Performance by Fuzzy Formulation Strategy

C. J. Shih This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and T. J. Tseng¹

¹Department of Mechanical Engineering Tamkang University Tamsui, Taipei, Taiwan, R.O.C.

Received: March 12, 2001
Accepted: March 29, 2001
Publication Date: March 29, 2001

Download Citation: ||https://doi.org/10.6180/jase.2001.4.1.07

ABSTRACT

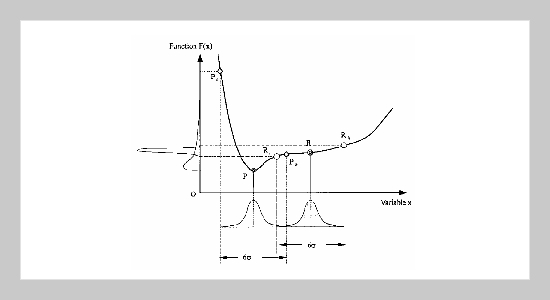
This paper presents an optimum design methodology for obtaining the highest robust performance using fuzzy multi-objective formulation strategy. The target performance and its variation, as functions of normally distributed variables with stochastic independence, are simultaneously minimized in this design process. A functional representation of the variability of the performance and the computational algorithm of the robust design process are presented in the paper. Two categories of design problems are examined: (1) the robust design with expected target of minimal variation. (2) The robust design with optimized target of minimal variation. The strength-based reliability behaves as the design objective that was merged in the formulation to extend the application of the proposed method. Three mechanical design examples further illustrate the presented integrated design methodology and successfully show its advantage.

Keywords: Robust Mechanical Design, Variability Optimization, Mean and Variance, Fuzzy Formulation, Engineering Design

REFERENCES

[1] Chang, H., “A Simple Computer-Aided Design Procedure for Minimal Variations,” Computer Methods in Applied Mechanics and Engineering, Vol. 73, pp. 99-107 (1989).
[2] Chang, H., “Design for Minimal System performance Deviation,” Proceedings of the ASME International Computers in Engineering conference and Exposition, C.A., USA, pp. 495-501 (1989).
[3] D'Errico, J. R. and Zaino, Jr. N. A., “Statistical Tolerancing Using a Modification to Taguchi's Method,” Technometrics, vol. 30, No. 4, pp. 397-405 (1988).
[4] Eggert, R. J. and Mayne, R. W., “Probabilistic Optimal Design Using Successive Surrogate probability Density Functions,” Proceedings of the ASME Design Automation Conference, DE-23-1, pp. 129-136 (1990).
[5] Eschenauer, H., Koski, J and Osyczka, A., Multicriteria Design optimization- Procedures and Applications, Springer-Verlag, (1990).
[6] Parkinson, D. B., “Control and Optimization of Variability,” Reliability Engineering, Vol. 19, pp. 211-236 (1987).
[7] Parkinson, D. B., “Robust Design by Variability Optimization,” Quality And Reliability Engineering International, Vol. 13, pp. 97-102 (1997).
[8] Rao, S. S., “Multiple-objective Optimization of Fuzzy Structure System,” International Journal for Numerical Method in Engineering, Vol. 24, pp. 1157-1171 (1987).
[9] Rao, S. S., Reliability-Based Optimum Design, McGraw-Hill Book Company, (1992).
[10]Ross, P. J., Taguchi Techniques for Quality Engineering, McGraw-Hill Book Company, (1988).
[11]Shih, C. J., Liu, Woe-Chun and Wangsawidjaja, R.A.S., “Reliability-Based Optimization and Application of Fuzzy Theory for Robust Structural Design,” Tamkang Journal of Science and Engineering, Vol. 1, No. 1, July, pp. 31-37 (1998).
[12]Shih, C. J. and Wangsawidjaja, R.A.S., “Multiobjective Fuzzy Optimization with Random Variable in a Mix of Fuzzy and Probabilistic Environment,” The Joint Conference of the 4th Fuzzy-IEEE/Ifes’95, Yokohama, Japan, March, 20-24 (1995).
[13]Taguchi, G. and Wu, Y., Introduction to Off-line Quality Control, Tokyo, Japan, Central japan Quality Control Association, (1979).
[14]Vanderplaats, G. N., Numerical Optimization Techniques for Engineering Design -with Applications, Internatial edition, McGraw-Hill (1993).
[15]Yu, J. and Ishii, K., “A Robust Optimization Method for Systems with Significant Nonlinear Effects,” Advance in Design Automation, DE-65-1, ASME, pp. 371-378 (1993).