Quantized Output Observer-based Data Driven Model-free Adaptive Control

Bing  Ren; Guangqing  Bao

doi:10.6180/jase.202402_27(2).0004

Quantized Output Observer-based Data Driven Model-free Adaptive Control

Computer Science and Information Engineering

Bing Ren^1,2 , Guangqing Bao³This email address is being protected from spambots. You need JavaScript enabled to view it.

¹College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou, China

²School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou, China

³School of Electronics & Information Engineering, Southwest Petroleum University, Chengdu, China

Received: December 5, 2022
Accepted: March 13, 2023
Publication Date: June 17, 2023

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202402_27(2).0004

This paper studies the quantized output data observer-based data-driven model-free adaptive control(qMFAC) for discrete-time nonlinear systems with unknown structures and network transmission constraints. First, an adaptive observer based on quantized output data is generated with the use of a logarithmic quantizer, and a pseudo-biased derivative(PPD) estimation scheme based on the output quantized data observer is proposed. By dynamic linearization(DL) techniques, a incomplete equivalent data model containing quantized output data are built. Then, the observer output is used to develop a data-driven model-free adaptive control strategy that only makes use of quantified output and input. With the Lyapunov function and sector boundary approaches, the bounded tracking performance of the proposed qMFAC is strictly theoretical analyzed, and the effectiveness of qMFAC is verified through numerical simulation and simulation experiments of the shell and tube heat exchanger control system.

Keywords: Quantized output data; Adaptive observer; Data-driven; Logarithmic quantizer; Pseudo-partial derivative;

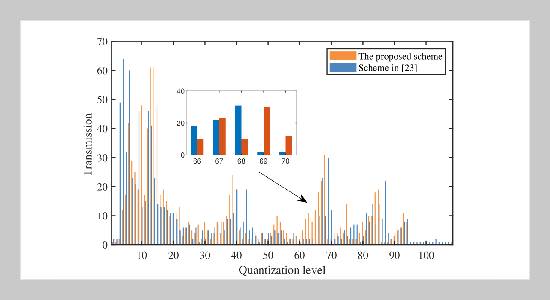
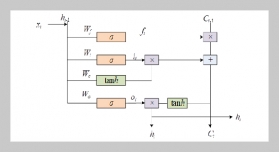
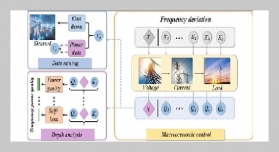
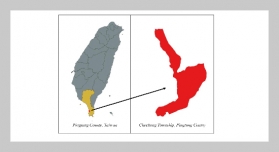
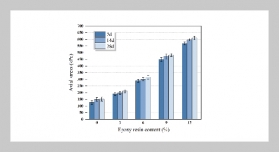
[1] X. Chu and M. Li, (2018) “Event-triggered fault estimation and sliding mode fault-tolerant control for a class of nonlinear networked control systems" Journal of the Franklin Institute 355(13): 5475–5502.
[2] C. Peng, J. Zhang, and Q.-L. Han, (2018) “Consensus of multiagent systems with nonlinear dynamics using an integrated sampled-data-based event-triggered communication scheme" IEEE Transactions on Systems, Man, and Cybernetics: Systems 49(3): 589–599.
[3] H. Liang, L. Chen, Y. Pan, and H.-K. Lam, (2022) “Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative-antagonistic interactions" IEEE Transactions on Fuzzy Systems:
[4] Z. Cao, B. Niu, G. Zong, and N. Xu, (2023) “Smallgain technique-based adaptive output constrained control design of switched networked nonlinear systems via event-triggered communications" Nonlinear Analysis: Hybrid Systems 47: 101299.
[5] X. Liu, J. Zhang, and Y. Xia, (2019) “Co-design of quantization and event-driven control for networked control systems" IEEE Transactions on Systems, Man, and Cybernetics: Systems 51(5): 3103–3110.
[6] L. Cao, Y. Pan, H. Liang, and T. Huang, (2022) “Observer-Based Dynamic Event-Triggered Control for Multiagent Systems With Time-Varying Delay" IEEE Transactions on Cybernetics:
[7] F. Cheng, H. Wang, L. Zhang, A. Ahmad, and N. Xu, (2022) “Decentralized adaptive neural two-bit-triggered control for nonstrict-feedback nonlinear systems with actuator failures" Neurocomputing 500: 856–867.
[8] L. Xing, C. Wen, H. Su, J. Cai, and L. Wang, (2015) “A new adaptive control scheme for uncertain nonlinear systems with quantized input signal" Journal of the Franklin Institute 352(12): 5599–5610.
[9] S. Song, J. H. Park, B. Zhang, and X. Song, (2021) “Composite adaptive fuzzy finite-time quantized control for full state-constrained nonlinear systems and its application" IEEE Transactions on Systems, Man, and Cybernetics: Systems 52(4): 2479–2490.
[10] X. Song, M. Wang, C. K. Ahn, and S. Song, (2021) “Finite-time fuzzy bounded control for semilinear PDE systems with quantized measurements and markov jump actuator failures" IEEE Transactions on Cybernetics 52(7): 5732–5743.
[11] B. Xuhui, W. Taihua, H. Zhongsheng, and C. Ronghu, (2015) “Iterative learning control for discrete-time systems with quantised measurements" IET Control Theory & Applications 9(9): 1455–1460.
[12] X. Cai, K. Shi, S. Zhong, and X. Pang, (2021) “Dissipative sampled-data control for high-speed train systems with quantized measurements" IEEE Transactions on Intelligent Transportation Systems 23(6): 5314–5325.
[13] D. Shen and C. Zhang, (2020) “Zero-error tracking control under unified quantized iterative learning framework via encoding–decoding method" IEEE Transactions on Cybernetics 52(4): 1979–1991.
[14] X. Chu and M. Li, (2019) “Integrated event-triggered fault estimation and fault-tolerant control for discretetime fuzzy systems with input quantization and incomplete measurements" Journal of the Franklin Institute 356(13): 7112–7143.
[15] S. Ha, L. Chen, H. Liu, and S. Zhang, (2022) “Command filtered adaptive fuzzy control of fractional-order nonlinear systems" European Journal of Control 63: 48–60.
[16] H. Qiu, H. Liu, and X. Zhang, (2022) “Composite adaptive fuzzy backstepping control of uncertain fractionalorder nonlinear systems with quantized input" International Journal of Machine Learning and Cybernetics: 1–15. DOI: 10.1007/s13042-022-01666-9.
[17] Y. Xu, D. Shen, and X. Bu, (2017) “Zero-error convergence of iterative learning control using quantized error information" IMA Journal of Mathematical Control and Information 34(3): 1061–1077.
[18] D. Shen and Y. Xu, (2016) “Iterative learning control for discrete-time stochastic systems with quantized information" IEEE/CAA Journal of Automatica Sinica 3(1): 59–67.
[19] S. Lee and H.-J. Song, (2021) “Accurate statistical model of radiation patterns in analog beamforming including random error, quantization error, and mutual coupling" IEEE Transactions on Antennas and Propagation 69(7): 3886–3898.
[20] S. Liu, B. Niu, G. Zong, X. Zhao, and N. Xu, (2022) “Data-driven-based event-triggered optimal control of unknown nonlinear systems with input constraints" Nonlinear Dynamics 109(2): 891–909.
[21] Z. Hou and S. Jin, (2010) “A novel data-driven control approach for a class of discrete-time nonlinear systems" IEEE Transactions on Control Systems Technology 19(6): 1549–1558.
[22] Y. Zhao, X. Liu, H. Yu, and J. Yu, (2020) “Model-free adaptive discrete-time integral terminal sliding mode control for PMSM drive system with disturbance observer" IET Electric Power Applications 14(10): 1756–1765.
[23] X. Bu, Y. Qiao, Z. Hou, and J. Yang, (2018) “Model free adaptive control for a class of nonlinear systems using quantized information" Asian Journal of Control 20(2): 962–968.
[24] H. Zhang, J. Zhou, Q. Sun, J. M. Guerrero, and D. Ma, (2015) “Data-driven control for interlinked AC/DC microgrids via model-free adaptive control and dual-droop control" IEEE Transactions on Smart Grid 8(2): 557–571.
[25] Y. Weng and X. Gao, (2016) “Data-driven robust output tracking control for gas collector pressure system of coke ovens" IEEE Transactions on Industrial Electronics 64(5): 4187–4198.
[26] S. Zhang, P. Zhou, Y. Xie, and T. Chai, (2022) “Improved model-free adaptive predictive control method for direct data-driven control of a wastewater treatment process with high performance" Journal of Process Control 110: 11–23.
[27] D. Xu, Y. Shi, and Z. Ji, (2017) “Model-free adaptive discrete-time integral sliding-mode-constrained-control for autonomous 4WMV parking systems" IEEE Transactions on Industrial Electronics 65(1): 834–843.
[28] X. Li, C. Ren, S. Ma, and X. Zhu, (2020) “Compensated model-free adaptive tracking control scheme for autonomous underwater vehicles via extended state observer" Ocean Engineering 217: 107976.
[29] X. Bu, P. Zhu, Q. Yu, Z. Hou, and J. Liang, (2020) “Model-free adaptive control for a class of nonlinear systems with uniform quantizer" International Journal of Robust and Nonlinear Control 30(16): 6383–6398. [30] H. Zhao, L. Peng, and H. Yu, (2022) “Quantized modelfree adaptive iterative learning bipartite consensus tracking for unknown nonlinear multi-agent systems" Applied Mathematics and Computation 412: 126582.