Robust Confidence Interval Estimation Method for the Mean of Poisson Distribution to Handle Outliers

Juthaphorn Sinsomboonthong; Saichon Sinsomboonthong

doi:10.6180/jase.202208_25(4).0020

Robust Confidence Interval Estimation Method for the Mean of Poisson Distribution to Handle Outliers

Physics

Juthaphorn Sinsomboonthong This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Saichon Sinsomboonthong²

¹Department of Statistics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand
²Department of Statistics, School of Science, King Mongkut’s Institute of Technology Ladkrabang, Bangkok 10520, Thailand

Received: July 31, 2021
Accepted: October 18, 2021
Publication Date: December 6, 2021

Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Download Citation: ||https://doi.org/10.6180/jase.202208_25(4).0020

ABSTRACT

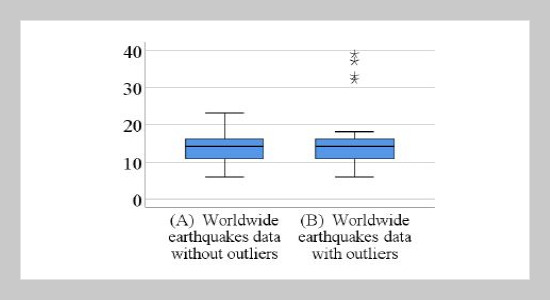
In this article, the robust confidence interval estimation method for the Poisson mean to handle outliers in data set is presented. The proposed technique is called median bootstrap confidence interval or BC−Med method. The simulation study was constructed 160 situations to compare the efficiency for two criteria—the coverage probability and the average width—of five methods, namely, Wald, WaldC, Bégaud, Brown and BC−Med methods. It is found that in case of non-outliers in the data set, Brown method tends to have the desirable performance for almost all levels of the Poisson means and all sample sizes n. Furthermore, the efficiency of Wald method is also as good as that of Brown method for the sample sizes are not less than 30 and almost all levels of the Poisson means when data set is not contaminated with outliers. In case of outliers in the data set, BC−Med method tends to have the most efficiency for all levels of sample sizes n and almost all levels of the Poisson means. The findings will be useful for researchers to more accurately estimate the mean of Poisson distribution when sample data are contaminated with outliers, e.g., estimation of the number of deaths from accidents per day. Because the BC−Med method was developed from a robust location estimator, therefore outliers have slightly influence on the Poisson mean estimation for this proposed method.

Keywords: average width; bootstrap confidence interval; coverage probability; Poisson mean

REFERENCES

[1] M.-H.Wu, J.Wang, and K.-W. Ku, (2019) “Earthquake, Poisson and Weibull distributions" Physica A: Statistical Mechanics and its Applications 526: 121001. DOI:10.1016/j.physa.2019.04.237.
[2] M. A. Raza and M. Aslam, (2019) “Design of control charts for multivariate Poisson distribution using generalized multiple dependent state sampling" Quality Technology & Quantitative Management 16(6): 629–650. DOI: 10.1080/16843703.2018.1497935.
[3] B. Jarosz, (2021) “Poisson distribution: A model for estimating households by household size" Population Research and Policy Review 40(2): 149–162. DOI: 10.1007/s11113-020-09575-x.
[4] P. Puig and C. H. Weiß, (2020) “Some goodness-of-fit tests for the Poisson distribution with applications in Biodosimetry" Computational statistics & data analysis 144: 106878. DOI: 10.1016/j.csda.2019.106878.
[5] U. N. Bhat. “Queueing networks”. In: An Introduction to queueing theory. Springer, 2015, 159–176.
[6] O. Ibe. Markov processes for stochastic modeling. Newnes, 2013. DOI: 10.1016/C2012-0-06106-6.
[7] J. Sinsomboonthong and S. Sinsomboonthong, (2021) “Weighted Maximum Likelihood Correlation Coefficient to Handle Missing Values and Outliers in Data Set" Wseas Transactions On Mathematics 20: 415–430. DOI: 10.37394/23206.2021.20.43.
[8] J. Neyman, (1937) “Outline of a theory of statistical estimation based on the classical theory of probability" Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 236(767): 333–380.
[9] N. C. Schwertman and R. A. Martinez, (1994) “Approximate Poisson confidence limits" Communications in statistics-theory and methods 23(5): 1507–1529. DOI: 10.1080/03610929408831336.
[10] T. T. Cai, (2005) “One-sided confidence intervals in discrete distributions" Journal of Statistical planning and inference 131(1): 63–88. DOI: 10.1016/j.jspi.2004.01.005.
[11] J. C. Correa, (2007) “Interval Estimation for the Poisson Distribution Parameter with a Single Observation" Revista Colombiana de Estadistica 30(1): 69–75.
[12] B. Bégaud, K. Martin, A. Abouelfath, P. Tubert-Bitter, N. Moore, and Y. Moride, (2005) “An easy to use method to approximate Poisson confidence limits" European journal of epidemiology 20(3): 213–216. DOI:10.1007/s10654-004-6517-4.
[13] L. Barker, (2002) “A comparison of nine confidence intervals for a Poisson parameter when the expected number of events is⩽ 5" The American Statistician 56(2): 85–89. DOI: 10.1198/000313002317572736.
[14] A. M. Pires and C. Amado, (2008) “Interval estimators for a binomial proportion: Comparison of twenty methods" REVSTAT–Statistical Journal 6(2): 165–197.
[15] M. B. Swift, (2009) “Comparison of confidence intervals for a Poisson mean–further considerations" Communications in Statistics-Theory and Methods 38(5): 748–759. DOI: 10.1080/03610920802255856.
[16] L. D. Brown, T. T. Cai, and A. DasGupta, (2003) “Interval estimation in exponential families" Statistica Sinica: 19–49.
[17] V. Patil and H. Kulkarni, (2012) “Comparison of confidence intervals for the Poisson mean: some new aspects" REVSTAT–Statistical Journal 10(2): 211–227.
[18] B. Efron and R. J. Tibshirani. An introduction to the bootstrap. CRC press, 1994.
[19] J. Chen and H. Rubin, (1986) “Bounds for the difference between median and mean of gamma and Poisson distributions" Statistics & probability letters 4(6): 281–283. DOI: 10.1016/0167-7152(86)90044-1.
[20] H. Liero and S. Zwanzig. Introduction to the theory of statistical inference. CRC press, 2016.
[21] M. F. Freeman and J. W. Tukey, (1950) “Transformations related to the angular and the square root" The Annals of Mathematical Statistics: 607–611.
[22] A. Gelman, (2009) “Bayes, Jeffreys, prior distributions and the philosophy of statistics" Statistical Science 24(2): 176–178. DOI: 10.1214/09-STS284D.
[23] J. Carpenter and J. Bithell, (2000) “Bootstrap confidence intervals: when, which, what? A practical guide for medical statisticians" Statistics in medicine 19(9): 1141–1164.
[24] A. C. Davison and D. V. Hinkley. Bootstrap methods and their application. 1. Cambridge university press, 1997.
[25] B. Ghosh, (1979) “A comparison of some approximate confidence intervals for the binomial parameter" Journal of the American Statistical Association 74(368): 894–900. DOI: 10.1080/01621459.1979.10481051.
[26] URL: https ://www.usgs.gov/natural - hazards/earthquake-hazards/lists-maps-and-statistics..
[27] P. G. Andersson, (2015) “A classroom approach to the construction of an approximate confidence interval of a Poisson mean using one observation" The American Statistician 69(3): 160–164. DOI: 10.1080/00031305.2015.1056830.
[28] A. Shirvani and M. Fathizadeh, (2020) “Assessing the Accuracy of Approximate Confidence Intervals Proposed for the Mean of Poisson Distribution" Journal of Modern Applied Statistical Methods 18(1): 3. DOI:10.22237/jmasm/1556668800.