Kuo-Ming Hung This email address is being protected from spambots. You need JavaScript enabled to view it.¹, Ching-Tang Hsieh², Cheng-Hsiang Yeh² and Li-Ming Chen¹

¹Department of Information Management, Kainan University, Taoyuan, Taiwan 338, R.O.C.
²Department of Electrical Engineering, Tamkang University, Tamsui, Taiwan 251, R.O.C.

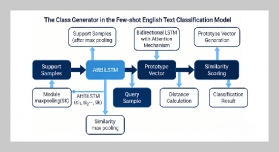
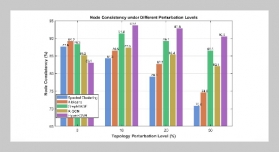
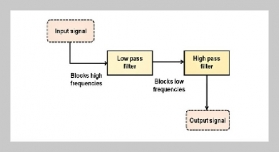
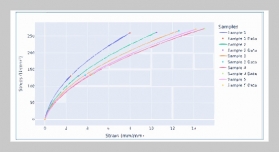
REFERENCES

1. [1] Shih, T. K. and Chang, R. C., “Digital Inpainting — Survey and Multilayer Image Inpainting Algorithms,” Proc. IEEE Int. Conf. Inform. Tech. Appl., Vol. 1, pp. 15-24 (2005).
2. [2] Bertalmio, M., Sapiro, G., Caselles, V. and Ballester, C., “Image Inpainting,” SIGGRAPH, pp. 417
   424 (2000).
3. [3] Telea, A., “An Image Inpainting Technique Based on the Fast Marching Method,” Journal of Graphics Tools, Vol. 9, ACM Press, pp. 25
   36 (2004).
4. [4] Zhou, T., Tang, F., Wang, J., Wang, Z. and Peng, Q., “Digital Image Inpainting with Radial Basis Functions,” J. Image Graphics, pp. 1190
   1196 (2004).
5. [5] Liew, A. W. C., Law, N. F. and Nguyen, D. T., “Multiple Resolution Image Restoration,” IEE Proceedings - Vision, Image and Signal Processing, Vol. 144, pp. 199
   206 (1997).
6. [6] Burrus, C. S., Gopinath, R. A. and Guo, H., Introduction to Wavelets and Wavelet Transform, Prentice-Hall (1998).
7. [7] Chen, Y. L., Hsieh, C. T. and Hsu, C. H., “Progressive Image Inpainting Based on Wavelet Transform,” IEICE, Trans. Fund., Vol. E88-A, pp. 2826
   2834 (2005).
8. [8] Le Pennec, E. and Mallat, S., “Sparse Geometrical Image Representation with Bandelets,” IEEE Trans. Image Process, Vol. 14, pp. 423
   438 (2005).
9. [9] Le Pennec, E. and Mallat, S., “Bandelet Image Approximation and Compression,” SIAM J. Multiscale Simul., Vol. 4, pp. 992
   1039 (2005).
10. [10] Hung, K. M., Chen, Y. L. and Hsieh, C. T. “A Novel Bandelet-Based Image Inpainting,” IEICE TRANSACTIONS on Fundamentals of Electronics, Communications and Computer Sciences, Vol. E92-A, pp. 2471
    2478 (2009). (SCI)
11. [11] Grattoni, P., Pollastri, E. and Premoli, A., “A Contour Detection Algorithm Based on the Minimum Radial Inertia (MRI) Criterion,” CVGIP, Vol. 43, pp. 22
    36 (1988).
12. [12] Eslami, R. and Radha, H., “Wavelet-Based Contourlet Transform and Its Application to Image Coding,” IEEE Intl. Conf. on Image Processing, pp. 3189
    3192 (2004).
13. [13] Olshausen, B. A., Sallee, P. and Lewicki, M. S., “Learning Sparse Image Codes Using a Wavelet Pyramid Architecture,” Advances in Neural Information Processing Systems 13, MIT Press: Cambridge, MA, pp. 887
    893 (2000).
14. [14] Burt, P. J. and Adelson, E. H., “The Laplacian Pyramid as a Compact Image Code,” IEEE Trans. Commun., Vol. 31, pp. 532
    540 (1983).
15. [15] Adelson, E. H., Anderson, C. H., Bergen, J. R., Burt, P. J., Ogden, J. M., “Pyramid Methods in Image Processing,” RCA Engineer, Vol.29, pp. 33
    41 (1984).
16. [16] Donoho, D., “Wedgelets: Nearly-Minimax Estimation of Edges,” Ann. Statist., Vol. 27, pp. 353
    382 (1999).
17. [17] Belloulate, K. and Konard, J., “Fractal Image Compression with Region-Based Functionality,” IEEE Trans on Image Proc., Vol. 2, pp. 345
    350 (2002).
18. [18] Fisher, Y., Fractal Image Compression, SpringerVerlag, New York (1995).
19. [19] El Rube, I. A., Ahmed, M., Kamel, M., “Coarse-toFine Multiscale Affine Invariant Shape Matching and Classification,” Proceedings of the Pattern Recognition, 17th International Conference on (ICPR’04), Vol. 2, pp. 163
    166 (2004).
20. [20] Ulichney, R., Digital Halftoning, The MIT Press (1987).
21. [21] Floyd, R. W. and Steinberg, L., “Adaptive Algorithm for Spatial Grey Scale,” SID Int. Sym. Digest of Tech. Papers, pp. 36-37 (1975).
22. [22] Javis, J. F., Judice, C. N. and Ninke, W. H., “A Survey of Techniques for the Display of Continuous-Tone Pictures on Bilevel Displays,” Computer Graphics and Image Processing, Vol. 5, pp. 13
    40 (1976).
23. [23] Stucki, P., “MECCA
    A Multiple Error Correcting Computation Algorithm for Bilevel Image Hardcopy Reproduction,” Research Report RZ1060, IBM Research Laboratory (1981).
24. [24] Hein, S. and Zakhor, A., “Halftone to ContinuousTone Conversion of Error-Diffusion Coded Image,” IEEE Trans. Image Processing, Vol. 4, pp. 208
    216 (1995).
25. [25] Shen, M. Y. and Kuo, C.-C. J., “A Robust Nonlinear Filtering Approach to Inverse Halftoning,” J. Vis. Commun. Image Represen., Vol. 12, pp. 84
    95 (2001).
26. [26] Neelamani, R., Nowak, R. and Baraniuk, R., “WinHD: Wavelet-Based Inverse Halftoning via Deconvolution,” IEEE Trans. on Image Process., October 2002. Submitted.
27. [27] Xiong, Z., Orchard, M. T. and Ramchandran, K., “Inverse Halftoning Using Wavelets,” IEEE Trans. Image Process., Vol. 8, pp. 1479
    1482 (1999).
28. [28] Dabov, K., Foi, A., Katkovnik, V. and Egiazarian, K., “Inverse Halftoning by Pointwise Shape-Adaptive DCT Regularized Deconvolution,” Proc. 2006 Int. TICSP Workshop Spectral Meth. Multirate Signal Process., SMMSP 2006, Florence (2006).
29. [29] Mese, M. and Vaidyanathan, P. P., “Look Up Table (LUT) Method for Inverse Halftoning,” IEEE Trans. Image Process., Vol. 10, pp. 1566
    1578 (2001).
30. [30] Chung, K.-L. and Wu, S.-T., “Inverse Halftoning Algorithm Using Edge-Based Lookup Table Approach,” IEEE Trans. on Image Process., Vol. 14, pp. 1583
    1589 (2005).