Effect of Porosity on Unsteady Poiseuille Flow of a Viscoelastic Fluid with Temperature Dependent Viscosity

Hazem Ali  Attia

doi:10.6180/jase.2009.12.2.14

Effect of Porosity on Unsteady Poiseuille Flow of a Viscoelastic Fluid with Temperature Dependent Viscosity

Mathematics / Statistics

Hazem Ali Attia This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Department of Mathematics, College of Science, Al-Qasseem University, P.O. Box 237, Buraidah 81999, KSA

Received: October 25, 2004
Accepted: March 12, 2005
Publication Date: June 1, 2009

Download Citation: ||https://doi.org/10.6180/jase.2009.12.2.14

ABSTRACT

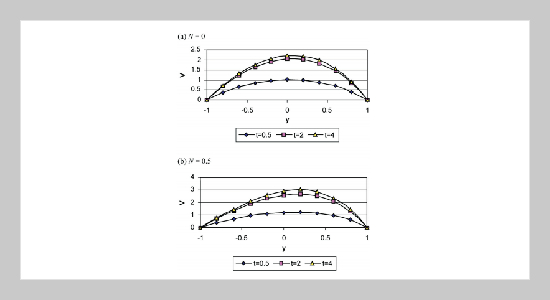
The unsteady Poiseuille flow of a viscoelastic fluid between two horizontal porous plates in the presence of a porous medium is studied with heat transfer. The fluid viscosity is assumed to be temperature dependent and the fluid is subjected to a uniform suction from above and injection from below. The plates are maintained at two fixed but different temperatures. The motion of the fluid is produced by a uniform horizontal constant pressure gradient. The equation of motion and the energy equation are solved numerically to yield the velocity and temperature distributions.

Keywords: Non-Newtonian Fluid, Heat Transfer, Variable Properties, Numerical Solution, Porous Medium

REFERENCES

[1] Hartmann, J. and Lazarus, F., Kgl. “Danske Videnskab. Selskab,” Mat.-Fys. Medd., Vol. 15, (1937).
[2] Sutton, G. W. and Sherman, A., “Engineering Magnetohydrodynamics,” (McGraw-Hill Book Co., 1965).
[3] Cramer, K. R. and Pai, S.-I., “Magnetofluid Dynamics for Engineers and Applied Physicists,” (McGraw-Hill Book Co., 1973).
[4] Alpher, R. A., “International Journal of Heat and Mass Transfer 3,” 108 (1961).
[5] Nigam, S. D and Singh, S. N., Quart. J. Mech. Appl. Math., Vol. 13, p. 85 (1960).
[6] Cho, Y. I. and Hartnett, J. P., “Non-Newtonian Fluids, Handbook of Heat Transfer Applications,” (McGrawHill Book Co., 1985).
[7] Hartnett, J. P., “Transactions of the ASME 114,” Vol. 296 (1992).
[8] Abel, M. S. and Idress, K. M., Indian J. of Theoretical Physics, Vol. 41, p. 1 (1993).
[9] Herwig, H. and Wicken, G., “Warme-Und Stoffubertragung 20,” 47 (1986).
[10] Klemp, K., Herwig, H. and Selmann, M., “Entrance Flow in Channel with Temperature Dependent Viscosity Including Viscous Dissipation Effects,” Proc. 3rd Int. Con. Fluid Mechanics, Cairo, Egypt 3, 1257 (1990).
[11] Carey, V. C. and Mollendorf, J. C., Int. J. “Heat Mass Transfer,” Vol. 23, p. 95 (1980).
[12] Martin, B. W., J. “Heat Fluid Flow,” 3, 122 (1973).
[13] Joseph, D. D., Nield, D. A. and Papanicolaou, G., Water Resources Research, Vol. 18, p. 1049 (1982).
[14] Ingham, D. B. and Pop, I., “Transport Phenomena in Porous Media,” (Pergamon, Oxford, 2002).
[15] Khaled, A. R. A. and Vafai, K., Int. J. Heat Mass Transf., Vol. 46, p. 4989 (2003).
[16] Skelland, A. H. P., “Non-Newtonian flow and heat transfer,” (John Wiley Book Co. 1967).
[17] Ames, W. F., “Numerical Solutions of Partial Differential Equations,” (2nd Ed. Academic Press, New York, 1977).