Che-Wun Chiou This email address is being protected from spambots. You need JavaScript enabled to view it.1 , Fu-Hua Chou1 , Su-Frang Shu1 and Jim-Min Lin2 1Department of Electronic Engineering, Ching Yun University, Chung-Li, Taiwan 320, R.O.C.
2Department of Information Engineering and Computer Science, Feng Chia University, Taichung, Taiwan 407, R.O.C.
Received:
January 13, 2005
Accepted:
June 1, 2005
Publication Date:
December 1, 2005
Download Citation:
||https://doi.org/10.6180/jase.2005.8.4.03
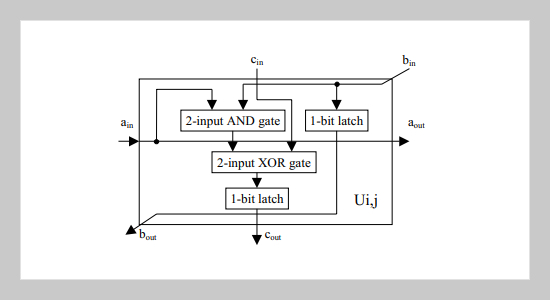
The natural fault-tolerant properties and regular structure of the Lee-Lu-Lee’s array multiplier over GF(2m) fields make it very attractive for VLSI implementation. However, the Lee-Lu-Lee’s array multiplier is time-consuming while comparing with other existing array multipliers. To overcome this problem, we will present a pipeline algorithm for such array multipliers with multiple speeds as comparing with the Lee-Lu-Lee’s array multiplier.ABSTRACT
Keywords:
Finite Fields Arithmetic, Modular Arithmetic, Public-Key Cryptosystem, Array Multiplier, Elliptic Curve Cryptosystem, Pipeline Processing
REFERENCES