Wei Ma This email address is being protected from spambots. You need JavaScript enabled to view it.¹, Weidong Song¹ and Linbin Qiu²

¹School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, P.R. China
²School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, P.R. China 

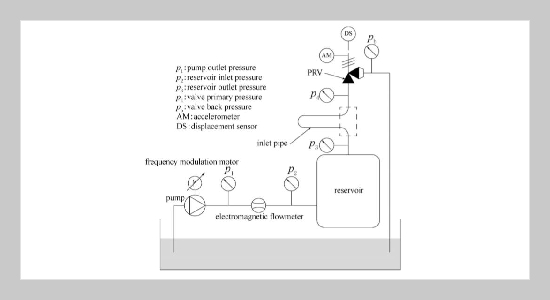
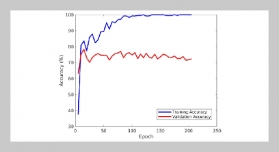
REFERENCES

1. [1] Yonezawa, K., R. Ogawa, K. Ogi, et al. (2012) Flow induced vibration of a steam control valve, Journal of Fluids & Structures 35(776), 7688. doi: 10.1016/j. jfluidstructs.2012.06.003
2. [2] Galbally, D., G. García, J. Hernando, et al. (2015) Analysis of pressure oscillations and safety relief valve vibrations in the main steam system of a boiling water reactor, Nuclear Engineering & Design 293(3), 258271. doi: 10.1016/j.nucengdes.2015.08.005
3. [3] Bolin, C., and A. Engeda (2015) Analysis of flow-induced instability in a redesigned steam control valve, Applied Thermal Engineering 83, 4047. doi: 10. 1016/j.applthermaleng.2015.02.043
4. [4] Wu, D., S. Li, and P. Wu (2015) CFD simulation of flow-pressure characteristics of a pressure control valve for automotive fuel supply system, Energy Conversion and Management 101, 658665. doi: 10.1016/ j.enconman.2015.06.025
5. [5] Mehrzad, S., I. Javanshir, A. R. Ranji, et al. (2015) Modeling of fluid-induced vibrations and identification of hydrodynamic forces on flow control valves, Journal of Central South University 22(7), 25962603. doi: 10.1007/s11771-015-2789-y
6. [6] Izuchi, H. (2010) Stability analysis of safety valve, 10th Topical Conference on Gas Utilization, pp.
7. [7] Wu, S., C. Li, and Y. Deng (2017) Stability analysis of a direct-operated seawater hydraulic relief valve under deep sea, Mathematical Problems in Engineering 2017, 1-11. doi: 10.1155/2017/5676317
8. [8] Song, X., L. Cui, M. Cao, et al. (2014) ACFD analysis of the dynamics of a direct-operated safety relief valve mounted on a pressure vessel, Energy Conversionand Management 81, 407419. doi: 10.1016/j.enconman. 2014.02.021
9. [9] Song, X. G., L. T. Wang, Y. C. Park, et al. (2015) A fluid-structure interaction analysis of the spring-loaded pressure safety valve during popping off, Procedia Engineering 130, 87-94. doi: 10.1016/j.proeng.2015. 12.178
10. [10] Vallet, C., J. Ferrari, J. F. Rit, et al. (2010) Single phase CFD inside a water safety valve, Proceedings of the Asme Pressure Vessels and Piping Conference, 335 342. doi: 10.1115/PVP2010-25619
11. [11] Beune, A., J. G. M. Kuerten, M. P. C. Van Heumen (2012) CFDanalysiswithfluid-structure interactionof opening high-pressure safety valves, Computers & Fluids 64, 108116. doi: 10.1016/j.compfluid.2012. 05.010
12. [12] Gabor, L., C. Alan, and H. Csaba (2009) Nonlinear analysis of a single stage pressure relief valve, IAENG International Journal of Applied Mathematics 39(4), 286299.
13. [13] Dechert, W. D., and R. Gencay (2010) Lyapunov exponents as a nonparametric diagnostic for stability analysis, Journal of Applied Econometrics 7(S1), S41 S60.
14. [14] Zamani, N., M. Ataei, and M. Niroomand (2015) Analysis and control of chaotic behavior in boost converter by ramp compensation based on Lyapunov exponents assignment: theoretical and experimental investigation, Chaos, Solitons &Fractals 81, 2029. doi: 10.1016/j.chaos.2015.08.010
15. [15] Di Bernardo, M., C. Budd, A. Champneys, et al. (2008) Bifurcations in nonsmooth dynamical systems, SIAM Review 50(4), 629701. doi: 10.1137/050625060
16. [16] Mason, J. F., P. T. Piiroinen, R. E. Wilson, et al. (2009) Basins of attraction in nonsmooth models of gear rattle, International Journal of Bifurcation and Chaos 19(1), 203224. doi: 10.1142/S021812740902283X
17. [17] Athanasios, I. M. (2012) Simulation and visualization ofchaoticsystems,Computer and Information Science 5(4), 2552.
18. [18] Bernardo, M. D. (2008) Piecewise-smooth Dynamical Systems: Theory and Applications, London: Springer.
19. [19] Strogatz, S. H. (2014) Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering.
20. [20] Ermentrout, B., and A. Simulating (2002) A guide to XPPAUT for researchers and students, Music & Letters 128(1), 309313.
21. [21] Liu, X. L., and D. O. Mathematics (2014) Application of XPPAUT software in the teaching of ‘ordinary differential equations’, College Mathematics 30(4), 117 122.
22. [22] Kong, W., and Q. Yi (2015) The application of XPPAUT in systems biology, Computers & Applied Chemistry 32(8), 938944.
23. [23] Lynch, S. (2014) Dynamical Systems with Applications Using Matlab, Switzerland: Birkhäuser Basel. doi: 10.1007/978-3-319-06820-6