Signal Sparse Representation Based on the Peak Transform and Modulus Maximum of Wavelet Coefficients

Yi-Gang Cen; Rui Xin; Xiao-Fang  Chen; Li-Hui  Cen; Ming-Xing Hu; Shi-Ming Chen

doi:10.6180/jase.2011.14.3.05

Signal Sparse Representation Based on the Peak Transform and Modulus Maximum of Wavelet Coefficients

Computer Science and Information Engineering

Yi-Gang Cen^1,2, Rui Xin^1,2, Xiao-Fang Chen This email address is being protected from spambots. You need JavaScript enabled to view it.³, Li-Hui Cen³ , Ming-Xing Hu⁴ and Shi-Ming Chen⁵

¹Institute of Information Science, Beijing Jiaotong University, Beijing, 100044, P.R. China
²Beijing Key Laboratory of Advanced Information Science and Network Technology, Beijing 100044, P.R. China
³School of Information Science and Engineering, Central South University, Hunan, Changsha 410083, P.R. China
⁴Centre for Medical Image Computing, University College London, UK
⁵School of Electrical and Electronic Engineering, East China Jiao Tong University, Jiangxi, Nanchang 330013, P.R. China

Received: December 17, 2010
Accepted: February 15, 2011
Publication Date: September 1, 2011

Download Citation: ||https://doi.org/10.6180/jase.2011.14.3.05

ABSTRACT

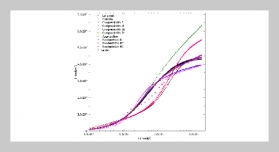
It is now well-known that one can reconstruct sparse or compressible signals accurately from a very limited number of measurements. This technique is known as “compressed sensing” or “compressive sampling” (CS). A basic requirement of CS is that a signal should be sparse or it can be sparsely represented in some orthogonal bases. Based on the Peak Transform (PT) and modulus maximum of wavelet coefficients, a new algorithm was proposed for the signals that are non-sparse themselves and can not be sparsely represented by wavelet transform such as the Linear Frequency Modulated signal. According to this algorithm, K-sparse wavelet coefficients can be obtained. For the peak sequence produced by the Peak Transform, value expansion approach of reversible watermarking is exploited such that the peak sequence can be embedded into the measurements of the signal, which avoids increasing additional points for transmission. By using the Peak Transform and modulus maximum, non-sparse wavelet coefficients can be transformed into K-sparse coefficients, which improves the reconstruction result of CS. Simulation results showed that our proposed algorithm achieved better performance comparing with the original CS algorithm.

Keywords: Compressed Sensing, Sparse Representation, Peak Transform, Modulus Maximum, Wavelet Transform

REFERENCES

[1] Donoho, D., “Compressed Sensing,” IEEE Trans. Inform. Theory, Vol. 52, pp. 12891306 (2006).
[2] Candes, E., “Compressive Sampling,” Proceedings of the International Congress of Mathmaticians, Madrid, Spain (2006).
[3] Candes, E. and Tao, T., “Near Optimal Signal Recovery From Random Projections: Universal Encoding Strategies?” IEEE Trans. Inform. Theory, Vol. 52, pp. 54065425 (2006).
[4] Candes, E. and Caltech J. R., l1-MAGIC: Recovery of Sparse Signals via Convex Programming, Oct., 2005; http://dsp.rice.edu/cs.
[5] He, Z. H., “Peak Transform for Efficient Image Representation and Coding,” IEEE Transactions on Image Processing, Vol. 16, pp. 17411754 (2007).
[6] Candes, E., Romberg, J. and Tao, T., “Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information,” IEEE Trans. Inform. Theory, Vol. 52, pp. 489509 (2006).
[7] Tropp, J. A. and Gilbert, A. C., “Signal Recovery from Random Measurements via Orthogonal Matching Pursuit,” IEEE Trans. Inform. Theory, Vol. 53, pp. 4655 4666 (2007).
[8] Donoho, D. and Tsaic, Y., “Extensions of Compressed Sensing,” Signal Processing, Vol. 86, pp. 533548 (2006).
[9] Tropp, J. A., “Greed is Good: Algorithmic Results for Sparse Approximation,” IEEE Trans. Inform. Theory, Vol. 50, pp. 22312242 (2004).
[10] Figueiredo, M. A. T., Nowak, R. D. and Wright, S. J., “Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problem,” Journal of Selected Topics in Signal Processing: Special Issue on Convex Optimization Methods for Signal Processing, Vol. 1, pp. 586598 (2007).
[11] Mallat, S. and Zhong, S., “Characterization of Signals from Multiscale Edges,” IEEE Trans. on PAMI, Vol. 14, pp. 710732 (1992).
[12] Zhao, R. Z., Song, G. X. and Qu, H. Z., “A New Piecewise Cubic Spline Interpolating Algorithm for the Reconstruction of Wavelet Coefficients,” Signal Processing (Chinese), Vol. 17, pp. 242277 (2001).

ABSTRACT

REFERENCES

Latest Articles