Jingzong Yang 1, Tianqing Yang1, and Chunchao Shi1
1School of Information, Baoshan University, BaoShan, Yunnan, 678000, P.R.China
Received:
April 16, 2021
Accepted:
June 16, 2021
Publication Date:
July 12, 2021
Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.
Download Citation: ||https://doi.org/10.6180/jase.202202_25(1).0008
ABSTRACT
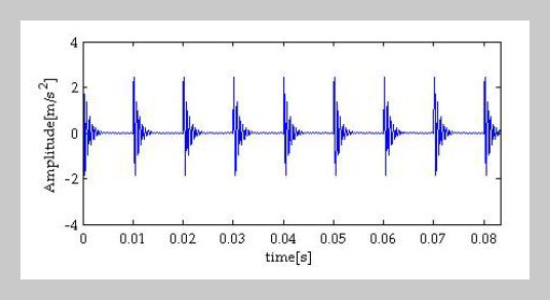
Rolling bearings are indispensable key components in mechanical equipment, and they are also one of the most easily damaged components. To solve the problem of bearing fault feature extraction under strong noise interference, a combination of complementary ensemble average empirical mode decomposition (CEEMD), total variation denoising (TVD) and multipoint optimal minimum entropy deconvolution adjusted(MOMEDA) is proposed. Firstly, decompose the vibration signal into several signal components. Secondly, the qualified IMF signal components are selected by combining with the cross-correlation analysis criteria for reconstruction, and TVD is used to reduce the noise of the signal. Thirdly, MOMEDA is used to filter the denoised signal, so as to enhance the periodic impact component. Finally, the envelope spectrum of the filtered signal is analyzed. The effectiveness of the proposed method is verified by the simulation signals and the bearing fault data set of Case Western Reserve University. The experimental results show that the proposed method can not only reduce the noise interference, but also effectively extract and identify the rolling bearing fault features. Compared with the results obtained by traditional LMD and ITD methods, it has better recognition effect.
Keywords:
Complementary ensemble average empirical mode decomposition (CEEMD); Total variation denoising (TVD); multipoint optimal minimum entropy deconvolution adjusted; fault feature extraction
REFERENCES
- [1] D. Griffin and J. Lim, (1984) “Signal estimation from modified short-time Fourier transform" IEEE Transactions on Acoustics, Speech, and Signal Processing 32(2): 236–243. DOI: 10.1109/TASSP.1984.1164317.
- [2] S. Qian and D. Chen, (1994) “Decomposition of the Wigner-Ville distribution and time-frequency distribution series" IEEE Transactions on Signal Processing 42(10): 2836–2842. DOI: 10.1109/78.324750.
- [3] W. Martin and P. Flandrin, (1985) “Wigner-Ville spectral analysis of nonstationary processes" IEEE Transactions on Acoustics, Speech, and Signal Processing 33(6): 1461–1470. DOI: 10.1109/TASSP.1985.1164760.
- [4] N. Hazarika, J. Z. Chen, A. C. Tsoi, and A. Sergejew, (1997) “Classification of EEG signals using the wavelet transform" Signal Processing 59(1): 61–72. DOI: https://doi.org/10.1016/S0165-1684(97)00038-8.
- [5] I. Daubechies, (1990) “The wavelet transform, timefrequency localization and signal analysis" IEEE Transactions on Information Theory 36(5): 961–1005. DOI: 10.1109/18.57199.
- [6] N. E. Huang, Z. Shen, S. R. Long, M. C. Wu, H. H. Shih, Q. Zheng, N. .-C. Yen, C. C. Tung, and H. H. Liu, (1998) “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis" Proceedings of the Royal Society of London Series A 454(1971): 903–998. DOI: 10.1098/rspa.1998.0193.
- [7] V. K. Mishra, V. Bajaj, A. Kumar, D. Sharma, and G. Singh, (2017) “An efficient method for analysis of EMG signals using improved empirical mode decomposition" AEU - International Journal of Electronics and Communications 72: 200–209. DOI: https://doi.org/10.1016/j.aeue.2016.12.008.
- [8] T. Guo and Z. Deng, (2017) “An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing" Applied Acoustics 127: 46–62. DOI: https://doi.org/10.1016/j.apacoust.2017.05.018.
- [9] W.Wang and X. Chen, (2018) “Vibration signal processing method for FOG based on improved EMD with masking signal" Dongnan Daxue Xuebao (Ziran Kexue Ban)/Journal of Southeast University (Natural Science Edition) 48: 1123–1129. DOI: 10.3969/j.issn.1001-0505.2018.06.020.
- [10] H. Fan, S. Shao, X. Zhang, X. Wan, X. Cao, and H. Ma, (2020) “Intelligent Fault Diagnosis of Rolling Bearing Using FCM Clustering of EMD-PWVD Vibration Images" IEEE Access 8: 145194–145206. DOI: 10.1109/ACCESS.2020.3012559.
- [11] J. Zheng and H. Pan, (2020) “Mean-optimized mode decomposition: An improved EMD approach for nonstationary signal processing" ISA transactions 106:392–401. DOI: 10.1016/j.isatra.2020.06.011.
- [12] J.-R. Yeh, J.-S. Shieh, and N. E. Huang, (2010) “Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method" Advances in adaptive data analysis 2(02): 135–156. DOI: 10 .1142/S1793536910000422.
- [13] J. Li, C. Liu, Z. Zeng, and L. Chen, (2015) “GPR signal denoising and target extraction with the CEEMD method" IEEE Geoscience and Remote Sensing Letters 12(8):1615–1619. DOI: 10.1109/LGRS.2015.2415736.
- [14] M. Zhou, K. Bian, F. Hu, andW. Lai, (2020) “A New Method Based on CEEMD Combined With Iterative Feature Reduction for Aided Diagnosis of Epileptic EEG" Frontiers in Bioengineering and Biotechnology 8:669.
- [15] S. Hou and W. Guo, (2020) “Optimal denoising and feature extraction methods using modified ceemd combined with duffing system and their applications in fault line selection of non-solid-earthed network" Symmetry 12(4):536.
- [16] L. I. Rudin, S. Osher, and E. Fatemi, (1992) “Nonlinear total variation based noise removal algorithms" Physica D: nonlinear phenomena 60(1-4): 259–268.
- [17] T. Sharma and K. K. Sharma, (2017) “QRS complex detection in ECG signals using locally adaptive weighted total variation denoising" Computers in biology and medicine 87: 187–199.
- [18] B. Yang, H. Xia, M. Annor-Nyarko, and Z. Wang, (2020) “Application of total variation denoising in nuclear power plant signal pre-processing" Annals of Nuclear Energy 135: 106981.
- [19] W. Smith and R. Randall, (2015) “Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study" Mechanical Systems and Signal Processing 64: 100–131. DOI: 10.1016/J.YMSSP.2015.04.021.
- [20] C. Zhou, J. Ma, J.Wu, and Z. Feng, (2019) “A parameter adaptive MOMEDA method based on grasshopper optimization algorithm to extract fault features" Mathematical Problems in Engineering 2019: